AGNES
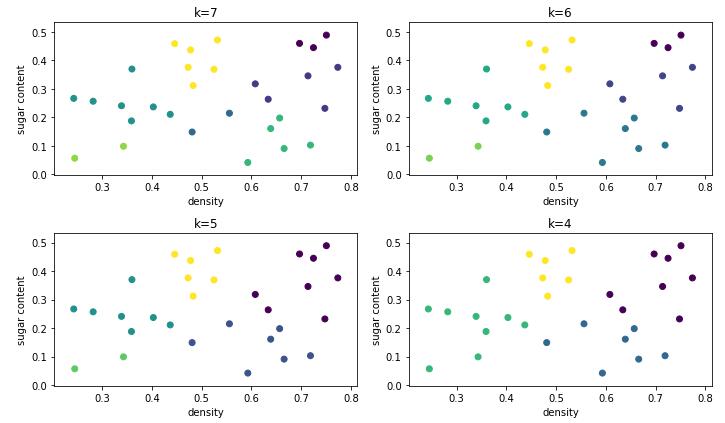
AGNES(AGglomerative NESting 的简写)是一种采用自底向上聚合策略的层次聚类算法。
【工作过程】:
先将数据集中的每个样本看作一个初始聚类簇;
然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并;
步骤(2)不断重复,直至达到预设的聚类簇的个数。
【关键】:如何计算聚类簇之间的距离。
实际上,每个簇是一个样本集合,因此,只需采用关于集合的某种距离即可。$$\text{最小距离:}d_{min}(C_i, C_j) = min_{x\in C_i,z\in C_j}dist(x,z)$$
$$\text{最大距离:}d_{max}(C_i, C_j) = max_{x\in C_i,z\in C_j}dist(x,z)$$
$$\text{平均距离:}d_{avg}(C_i, C_j) = \frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in C_j}dist(x,z)$$
显然,最小距离由两个簇的最近样本决定,最大距离由两个簇的最远样本决定,而平均距离则由两个簇的所有样本共同决定。
当 ...
学习向量量化 LVQ
学习向量量化(Learning Vector Quantization,简称 LVQ)与 K 均值算法类似,也是试图找到一组原型向量来刻画聚类结构,但与一般聚类算法不同的是,LVQ 假设数据样本带有类别标记,学习过程利用样本的这些监督信息来辅助聚类。
给定样本集 $D = {(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)}$,每个样本 $x_i$ 是由 m 个属性描述的特征向量 $(x_i^1, x_i^2, \cdots, x_i^m), y_i \in Y$ 是样本 $x_i$ 的类别标记。
【目标】:学得一组 m 维原型向量 ${p_1, p_2, \cdots, p_k}$,每个原型向量代表一个聚类簇,簇标记 $t_j \in Y$。
【算法描述】:
输入:样本集 $D = {(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)}$;原型向量个数 k,各原型向量预设的类别标记 ${t_1, t_2, \cdots, t_k}$;学习率 $\eta \in (0, 1)$。
输出:原型向量 ...
主成分分析 PCA
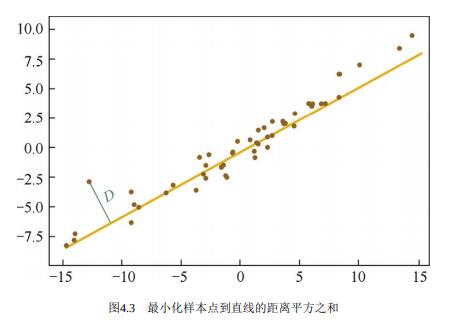
主成分分析(Principal Component Analysis,简称 PCA)是一种统计方法,通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量称为主成分。PCA 旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。
简单地说,PCA 就是要找出原始数据集中最主要的内容(特征),用这些内容来代替原始数据集。
【示例】:在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系 x,y,z 三个轴来表示数据,就需要使用三个维度。而实际上,这些点只出现在一个二维平面上,如果我们通过坐标系旋转变换(获得新坐标系)使得数据所在平面与 x,y 平面重合,那么我们就可以通过 x′,y′ 两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维。而 x′,y′ 两个轴所包含的信息就是我们要找到的主成分。
一般地,将原始数据集从 m 维降到 n 维(n < m)都会存在一定的损失,我们的目标是让损失尽可能地小。
【优点】:通过上面的介绍,我们可以归纳出 PCA 的优点。
降低数据的复杂性
识别最重要的多个特 ...