最近在研究中文拼写纠错，在查阅资料的时候看到了这篇文章《从编辑距离、BK树到文本纠错 - JadePeng - 博客园》，觉得 BK 树挺有意思的，决定深入研究一下，并在其基础上重新整理一遍，希望能够对各位读者大大们有所帮助。

前置知识

本节介绍实现基于 BK 树的中文拼写纠错候选召回所需要的前置知识，包括文本纠错的主流方案、编辑距离和 BK 树等相关概念。

文本纠错

目前业界主流的方案仍然是以 pipeline 的方式：“错误检测 -> 候选召回 -> 候选排序”的步骤依次进行。以平安寿险纠错方案（《NLP上层应用的关键一环——中文纠错技术简述》）为例，其系统整体架构如下图所示（侵权则删）：
pipeline 形式
整体上，平安寿险团队将纠错流程分解为错误检测 -> 候选召回 -> 候选排序三个关键步骤。

错误检测：为了解决资源受限问题以及音近错误问题，提出了基于字音混合语言模型的错误检测算法。该模型可以通过未标注的无监督原始语料进行训练，同时利用字音混合特征限制预测概率分布。
候选召回：结合双数组字典树以及 CSR 存储架构优化整体字典存储方案，同时优化内存空间及索引效果。此外，提出创新性的编辑距离召回算法，利用分层思想重构倒排索引字典存储方式，使得基于编辑距离的搜索变得灵活而高效。
候选排序：加入语言模型预测的语义特征，从而提高模型的判别能力。
本篇文章主要介绍基于 BK 树的方式来实现候选召回，对于错误检测和候选排序则不予以展开。

编辑距离

编辑距离（Edit Distance，又称莱温斯坦距离 Levenshtein Distance），是指 A、B 两个字符串，由 A 转成 B 所需的最少编辑操作次数。
其中，许可的编辑操作有替换、插入和删除。

替换：将一个字符替换成另一个字符。
插入：插入一个字符。
删除：删除一个字符。

一般来说，编辑距离越小，两个字符串的相似度越大。

A：实现替换操作
B：实现删除操作
A->B：
1. 替 -> 删
2. 换 -> 除
A->B的编辑距离 = 2

A：实现替换操作
B：实现换操作
A->B：
1. 删除“替”
A->B的编辑距离 = 1

关于编辑距离的实现，请参考 72. 编辑距离 - 力扣（LeetCode）。

BK 树

BK 树（Burkhard Keller Tree）是一种数据结构，其核心思想是：令 d(x,y) 表示字符串 x 到 y 的编辑距离。

d(x, y) = 0 当且仅当 x = y：编辑距离为 0 <==> 字符串相等。
d(x, y) = d(y, x)：从 x 变到 y 的最少步数等于从 y 变到 x 的最少步数。
d(x, y) + d(y, z) >= d(x, z)：从 x 变到 z 所需的步数不会超过 x 先变成 y 再变成 z 的步数，该性质被称为三角不等式，两边之和必然大于第三边。
在图像上，以词语作为节点，词语之间的距离作为边，从而构造一颗树，如下图所示。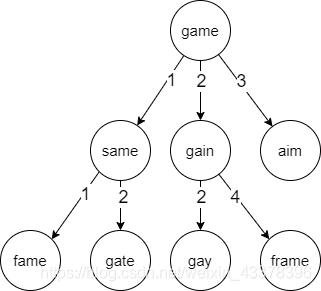
图1

基于 BK 树的数据结构，我们可以实现候选召回。例如，句子“It’s exactly the game as mine”，其中 game 应该修改为 same。当我们识别到 game 存在错误时，可以借助 BK 树（以编辑距离作为边），找到所有与 game 编辑距离为 1 的单词，例如 same、fame 和 gate，从而实现候选召回。

BK 树的优点在于将查询的时间复杂度从$O(n)$降低至$O(log(n))$，其中 n 为词表大小。
那么，如何构造一颗 BK 树，并借助构造好的 BK 树来查询单词指定编辑距离的其他单词呢？请看下文。

实现步骤

构造一颗 BK 树；
实现 BK 树查询逻辑。

具体实现的语言选择 python。

构造 BK 树

首先，定义 Node Class，作为树的节点。

class Node:

    def __init__(self, word: str):
        self.word = word
        self.branch = {}

Node Class 包含 word 和 branch 两个属性，word 表示节点的词语，branch 表示分支，以字典的形式进行存储，其中 key 为父子节点（词语）之间的编辑距离，value 为子节点。

接着，随机选择一个词语作为根节点，例如图 1 的 game；
然后，继续选择下一个词语，例如 same，计算它们之间的编辑距离，将 same 节点作为 game 根节点新的分支；
继续选择下一个词语，例如 fame，仍然从根节点开始遍历，计算 fame 和 game 的编辑距离，此时发现编辑距离 1 的分支已经存在了（same 与 game 的编辑距离为 1）！此时，沿着这条分支往下走，计算 fame 与 same 的编辑距离，而 same 节点没有编辑距离为 1 的分支，因此将 fame 挂载到 same 节点下，作为 same 节点的新分支。
依次选择余下的词语，按照步骤 2、3 不断扩展，从而构造出 BK 树。

【实现代码】：

import tqdm



class BKTree:

    def __init__(self):
        self.root = None
        self.word_list = []

    def build(self, word_list: list) -> None:
        """
        构建 BK 树
        :param word_list: list 词语列表，[game, fame, ..., time]
        :return: None
        """
        if not word_list:
            return None

        self.word_list = word_list

        # 首先，挑选第一个词语作为 BK 树的根结点
        self.root = Node(word_list[0])

        # 然后，依次往 BK 树中插入剩余的词语
        for word in tqdm.tqdm(word_list[1:]):
            self._build(self.root, word)

    def _build(self, parent_node: Node, word: str) -> None:
        """
        具体实现函数：构建 BK 树
        :param parent_node: Node 父节点
        :param word:        str  待添加到 BK 树的词语
        :return: None
        """
        dis = edit_distance(parent_node.word, word)

        # 判断当前距离（边）是否存在，若不存在，则创建新的结点；否则，继续沿着子树往下递归
        if dis not in parent_node.branch:
            parent_node.branch[dis] = Node(word)
        else:
            self._build(parent_node.branch[dis], word)


if __name__ == "__main__":
    word_list = ["game", "fame", "same", "frame", "gain", "gay", "gate", "home", "aim", "acm"] 
    bk_tree = BKTree() 
    bk_tree.build(word_list)

让我们再来观察一下图 1 以及 BK 树的构建过程，我们可以发现：根节点 game 分支 1 下的所有子孙节点和它的编辑距离都为 1，分支 2 下的所有子孙节点和它的编辑距离都为 2；同理，节点 fame 分支 1 下的所有子孙节点和它的编辑距离都为 1。这个性质很有用，在借助 BK 树进行查询时可以减少计算量，并且可以将高词频的词语放在 BK 树的顶部，而不常见的词语添加到 BK 树的底部，这样也能够减少计算量（为什么可以减少计算量，读者们可以先思考一下）。

【实现代码】：使 build() 函数支持输入词频字典。

def build(self, word_list: list or dict) -> None:
    """
    构建 BK 树
    :param word_list: list or dict 词语列表或者词频字典
    :return: None
    """
    if not word_list:
        return None

    # 如果是词频字典形式，则将其按照词频降序排列，得到词语列表
    if type(word_list) == dict:
        word_list = [item[0] for item in sorted(word_list.items(), key=lambda x: x[1], reverse=True)]
    self.word_list = word_list

    # 首先，挑选第一个词语作为 BK 树的根结点
    self.root = Node(word_list[0])

    # 然后，依次往 BK 树中插入剩余的词语
    for word in tqdm.tqdm(word_list[1:]):
        self._build(self.root, word)

【词频字典】：

word_count_dict = { 
    "game": 5, 
    "fame": 3, 
    "same": 7, 
    "frame": 2, 
    "gain": 1, 
    "gay": 1, 
    "gate": 3, 
    "home": 6, 
    "aim": 5, 
    "acm": 1 
}

BK 树查询
BK 树查询的本质是多叉树的遍历，找到与查询词语编辑距离在指定范围内的词语，例如找到与 same 编辑距离小于 2 的词语。该查询过程的难点在于剪枝的过程——即如何在当前节点上选择分支（node.branch）。

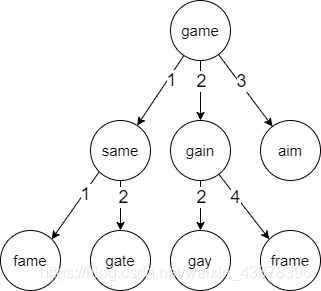图 1 图 1

以图 1 为例，要找到与 same 编辑距离小于 2 的词语，我们可以分两步走：

same 节点分支小于 2 的子树上的所有节点与 same 的编辑距离都小于 2，这是我们在上一小节构造 BK 树中发现的性质。
另一部分就比较麻烦了，可能是 same 的祖先节点，也可能在其他分支上，例如 gain 或者 aim 分支上面。这部分就需要遍历节点，然后依次计算查询词语（same）与各节点之间的编辑距离，并确定要不断遍历的分支。假设，在 BK 树的查询过程中，我们此时位于根节点 game，计算 same 与 game 的编辑距离为 1，满足条件，将 game 添加到返回结果中。接着，有三条分支可以走，那么问题来了，要选择哪几条分支呢？全都要，那就失去了 BK 树查询的优点，和线性查询没有区别。因此，我们需要挑选合适的分支，实现剪枝操作，从而减少计算量。那么到底该怎么做呢？

还记得 BK 树的核心思想吗？其中第三条，三角不等式性质！该性质是解决问题的关键（在查阅的资料中都一笔带过，没有详细讲解这一点，希望我这篇文章能够把其中的缘由介绍清楚）！我们的目标是找到 d(x, y) <= n 的所有词语，其中 y 是查询词语，x 是目标词语，n 是我们设定的编辑距离阈值。举个例子，gate 是查询词语，我们要找到与 gate 编辑距离为 3 的词语，通过图 1 可知 frame 和 aim 是目标词语（即我们要找到的词语）。我们沿着根节点不断遍历 BK 树，假设此时位于根节点 game，计算 gate 与 game 的编辑距离为 1。根据三角不等式性质，$n + d(gate, game) \geq d(game, branch)$，即$3 + d(gate, game) = 4 \geq d(frame, branch)$，换言之 game 节点 branch 小于等于 4 的分支都是满足条件的。

接着举例，我们继续往下遍历，走到 gain 节点，计算 d(gate, gain) = 2，那么$2 + d(gate, gain) = 4 \geq d(gain, branch)$，gain 节点 branch 小于等于 4 的分支都是满足条件的。往下走到达 frame，计算 frame 与 gate 的编辑距离为 3，将其添加到结果列表中。

上述过程解释起来仍然有些“绕”，让我们换个视角，看图 2（仍然沿用上述过程中使用的例子，gate 是查询词语，找到所有与 gate 编辑距离为 3 的词语）。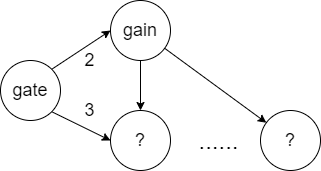
图 2 图 2

假设此时抵达了节点 gain，因为我们事先并不知道 gain 的所有子节点中是否存在与查询词语 gate 编辑距离为 3 的词语。为了不遗漏，最简单的做法就是全部遍历一遍，但这样处理的后果就是退化为了线性查询。因此，现在的目标是在不遗漏符合条件词语的前提下，尽可能减少需要遍历的分支。那么，我们可以假设，查询词语 gate 和 gain 的子节点中存在编辑距离为 3 的词语，从而确保不会遗漏。而 gate 和 gain 的编辑距离 d(gate, gain) = 2。根据三角不等式性质，$d(gain, ?) \leq d(gate, ?) + d(gate, gain)$，因此我们可以求出 d(gain, ?) 的值范围，从而确定接下来要遍历的分支，并且确保不会遗漏符合条件的词语。

【实现代码】：

def query(self, query_word: str, n: int) -> list:
    """
    BK 树查询
    :param query_word: str 查询词语
    :param n:          int 编辑距离
    :return: list 符合距离范围的词语列表
    """
    result = []

    self._traverse_judge_and_get(query_word, n, self.root, result)
    return result

def _traverse_judge_and_get(self, query_word: str, n: int, node: Node, result: list) -> None:
    """
    具体实现函数：BK 树查询
    :param query_word: str  查询词语
    :param n:          int  编辑距离
    :param node:       Node 当前节点
    :param result:     list 符合距离范围的词语列表
    :return: None
    """
    if not node:
        return None

    dis = edit_distance(query_word, node.word)

    # 根据三角不等式来确定查询范围，以实现剪枝的目的
    left, right = max(1, dis - n), dis + n
    
    # 若找到查询词语所在的节点，则直接将其所有子孙节点添加到 result 中
    if dis == 0:
        for dis in range(left, right + 1):
            if dis in node.branch and dis == n:
                self._traverse_and_get(node.branch[dis], result)                
        return None

    # 反之，则不断遍历节点，在查询范围内找到符合编辑距离范围的词语
    for dis_range in range(left, right + 1):
        if dis_range in node.branch:
            dis_branch = edit_distance(query_word, node.branch[dis_range].word)

            # 符合距离范围的词语，将其添加到 result 列表中
            if dis_branch == n:
                result.append(node.branch[dis_range].word)

            # 继续沿着子节点遍历，直到叶子节点
            self._traverse_judge_and_get(query_word, n, node.branch[dis_range], result)

def _traverse_and_get(self, node: Node, result: list) -> None:
    """
    遍历 BK 树并获取遍历节点的词语
    :param node:       Node 当前节点
    :param result:     list 符合距离范围的词语列表
    :return: None
    """
    if not node:
        return None

    result.append(node.word)

    for dis, node_branch in node.branch.items():
        self._traverse_and_get(node_branch, result)

在上述代码的基础上我们还可以做改进，将编辑距离阈值 n 扩展为一个由 min_dist 和 max_dist 组成的编辑距离范围。

【改进代码】：通过黄色字体将改进代码标识出来（CSDN 不显示，可以移步至我的飞书文档）。

def query(self, query_word: str, max_dist: int, min_dist: int = 0) -> list:
    """
    BK 树查询
    :param query_word: str 查询词语
    :param max_dist:   int 最大距离
    :param min_dist:   int 最小距离
    :return: list 符合距离范围的词语列表
    """
    result = []

    self._traverse_judge_and_get(query_word, max_dist, min_dist, self.root, result)
    return result

def _traverse_judge_and_get(self, query_word: str, max_dist: int, min_dist: int, node: Node, result: list) -> None:
    """
    具体实现函数：BK 树查询
    :param query_word: str  查询词语
    :param max_dist:   int  最大距离
    :param min_dist:   int  最小距离
    :param node:       Node 当前节点
    :param result:     list 符合距离范围的词语列表
    :return: None
    """
    if not node:
        return None

    dis = edit_distance(query_word, node.word)

    # 根据三角不等式来确定查询范围，以实现剪枝的目的
    left, right = max(1, dis - max_dist), dis + max_dist
        
    if dis == 0:
        for dis in range(left, right + 1):
            if dis in node.branch and min_dist <= dis <= max_dist:
                self._traverse_and_get(node.branch[dis], result)                
        return None

    for dis_range in range(left, right + 1):
        if dis_range in node.branch:
            dis_branch = edit_distance(query_word, node.branch[dis_range].word)

            # 符合距离范围的词语，将其添加到 result 列表中
            if min_dist <= dis_branch <= max_dist:
                result.append(node.branch[dis_range].word)

            # 继续沿着子节点遍历，直到叶子节点
            self._traverse_judge_and_get(query_word, max_dist, min_dist, node.branch[dis_range], result)

def _traverse_and_get(self, node: Node, result: list) -> None:
    """
    遍历 BK 树并获取遍历节点的词语
    :param node:       Node 当前节点
    :param result:     list 符合距离范围的词语列表
    :return: None
    """
    if not node:
        return None

    result.append(node.word)

    for dis, node_branch in node.branch.items():
        self._traverse_and_get(node_branch, result)

PS：我们也可以使用其他的距离公式来替换编辑距离，只要该距离公式符合 BK 树的核心思想即可。

此外，还记得在上一节留下的思考题吗？为什么将高词频的词语放在 BK 树的顶部，不常见的词语添加到 BK 树的底部，可以减少计算量？这是因为将高频词语放在 BK 树的顶部，能够更快找到高频词语所在的节点，这样就可以直接将该节点下符合条件分支的所有子孙节点都添加到结果列表中，而不需要再依次计算查询词语与各节点的编辑距离，从而减少了计算量。