学习向量量化（Learning Vector Quantization，简称 LVQ）与 K 均值算法类似，也是试图找到一组原型向量来刻画聚类结构，但与一般聚类算法不同的是，LVQ 假设数据样本带有类别标记，学习过程利用样本的这些监督信息来辅助聚类。

给定样本集 $D = {(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)}$，每个样本 $x_i$ 是由 m 个属性描述的特征向量 $(x_i^1, x_i^2, \cdots, x_i^m), y_i \in Y$ 是样本 $x_i$ 的类别标记。

【目标】：学得一组 m 维原型向量 ${p_1, p_2, \cdots, p_k}$，每个原型向量代表一个聚类簇，簇标记 $t_j \in Y$。

【算法描述】：

  • 输入：样本集 $D = {(x_1, y_1), (x_2, y_2), \cdots, (x_n, y_n)}$；原型向量个数 k，各原型向量预设的类别标记 ${t_1, t_2, \cdots, t_k}$；学习率 $\eta \in (0, 1)$。
  • 输出：原型向量 ${p_1, p_2, \cdots, p_k}$。
  • 过程：
  1. 从样本集 D 中随机选取样本作为原型向量（初始均值向量）；
  2. 在每一轮迭代中，随机选取一个样本，并计算该样本与各个原型向量的距离，然后确定簇标记；
  3. 根据样本和原型向量的类别标记是否一致来进行相应的更新：
    • 若簇标记相等，则将原型向量向该样本靠近；
      $$
      p’ = p_{j*} + \eta (x_i - p_{j*})
      $$
    • 若簇标记不相等，则将原型向量远离该样本；
      $$
      p’ = p_{j*} - \eta (x_i - p_{j*})
      $$
  4. 若满足算法的停止条件（指定的迭代次数），则将当前原型向量作为最终结果返回。

在学得的一组原型向量 ${p_1, p_2, \cdots, p_k}$ 后，即可实现对样本空间 X 的簇划分。之后，对任意样本 x，将其划入与其距离最近的原型向量所代表的簇中。换言之，每个原型向量 $p_i$ 定义了与之相关的一个区域 $R_i$，该区域中每个样本与 $p_i$ 的距离不大于它与其他原型向量 $p_{i’}(i’\neq i)$ 的距离，即

公式 1

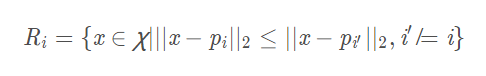
由此形成了对样本空间 X 的簇划分 ${R_1, R_2, \cdots, R_k}$，该划分通常称为 “Voronoi 剖分”（Voronoi tessellation）。若将 Ri 中样本全用原型向量 pi 表示。则可实现数据的“有损压缩”（lossy compression），这称为“向量量化”（vector quantization）；LVQ 由此而得名。

案例说明

构造一个数据集用以说明 LVQ 的执行过程，数据集内容如下：

1
2
3
4
5
[3, 4, 1]
[3, 3, 1]
[1, 2, 0]
[1, 1, 0]
[2, 1, 0]

前两列为样本的特征数据 X，最后一列为样本的标签值 Y。假设，此时我们将上述数据集划分为两个簇，并随机挑选 x1 和 x3 作为初始原型向量 p1 和 p2，学习率 $\eta = 0.1$。

在第一轮迭代中随机选取的样本 x2，分别计算 x2 与 p1 和 p2 的距离为 1 和 $\sqrt{5}$，x2 与 p1 距离更近且具有相同的标签值。
$$
p_1’ = p_1 + \eta \cdot (x_1-p_1) = (3; 4) + 0.1 * ((3; 3) - (3; 4)) = (3; 3.9)
$$
将 p1 更新为 p1’ 之后，不断重复上述过程，直到满足终止条件。

【存在问题】：若挑选 x1 和 x2 或 x3 和 x4 作为初始簇，那么我们最后得到的两个原型向量的标签值都是相同的，例如都为 0。这样就会导致无论输入的样本与哪个原型向量更接近，其标签值最终都为 0，这显然不是我们希望得到的结果。因此在挑选初始原型向量时需要将当前样本集的所有标签值都囊括在初始原型向量集中。

代码实现

【所需包】：

  • NumPy

【随机挑选初始均值向量函数】：随机确定起始位置，然后根据样本集长度和挑选数量计算出步长。这么做可以避免挑选出重复值，以及尽可能地从样本集各个区域挑选数据，而不是聚集在某一区域。

1
2
3
4
5
6
7
8
9
10
11
12
def random_select(dataset, count):
    # 获取样本集长度
    length = dataset.shape[0]
    # 计算步长和初始位置
    step, start = length // count, np.random.randint(length)
    data_select = []
    # 按照起始位置和步长挑选数据
    for i in range(count):        
        data_select.append(dataset[start])
        start += step
        start = start % length
    return data_select

【LVP 函数实现】：

  • 随机挑选指定数量的原型向量。
1
prototypes = random_select(dataset, k)
  • 开始迭代。
1
2
for i in range(n_iters):
    # ...
  • 迭代过程中，每次随机从样本集中选择一个样本，判断该样本所属的簇。
1
2
3
4
5
6
7
8
data = dataset[numpy.random.randint(length)]
    min_dist = numpy.inf
    cluster_index = -1
    for j in range(k):
        dist = numpy.linalg.norm(data[:2] - prototypes[j, :2], 2)**2
        if dist < min_dist:
            min_dist = dist
            cluster_index = j
  • 接着，判断当前样本的标签类别是否和所属簇的类别标签是否相同。根据不同的情况执行相应的操作。
1
2
3
4
if data[2] == prototypes[cluster_index, 2]:
    prototypes[cluster_index, :2] += learning_rate * (data[:2] - prototypes[cluster_index, :2])
else:
    prototypes[cluster_index, :2] -= learning_rate * (data[:2] - prototypes[cluster_index, :2])
  • 迭代结束后，返回原型向量。
1
return prototypes

【完整代码】：传送门

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def lvp(dataset, p, n_iters=100, learning_rate=1):
    length = dataset.shape[0]
    prototypes = random_select(dataset, p)
    
    for i in range(n_iters):
        # 随机挑选样本
        data_random = dataset[np.random.randint(length)]
        min_dist = np.inf
        cluster_index = -1
        # 判断当前样本所属的簇
        for j in range(p):
            dist = np.linalg.norm(data_random[:2] - prototypes[j, :2], 2)
            if dist < min_dist:
                min_dist = dist
                cluster_index = j
        if data_random[2] == prototypes[cluster_index, 2]:
            prototypes[cluster_index, :2] += learning_rate * min_dist
        else:
            prototypes[cluster_index, :2] -= learning_rate * min_dist
    return prototypes

参考

  • 《机器学习》周志华