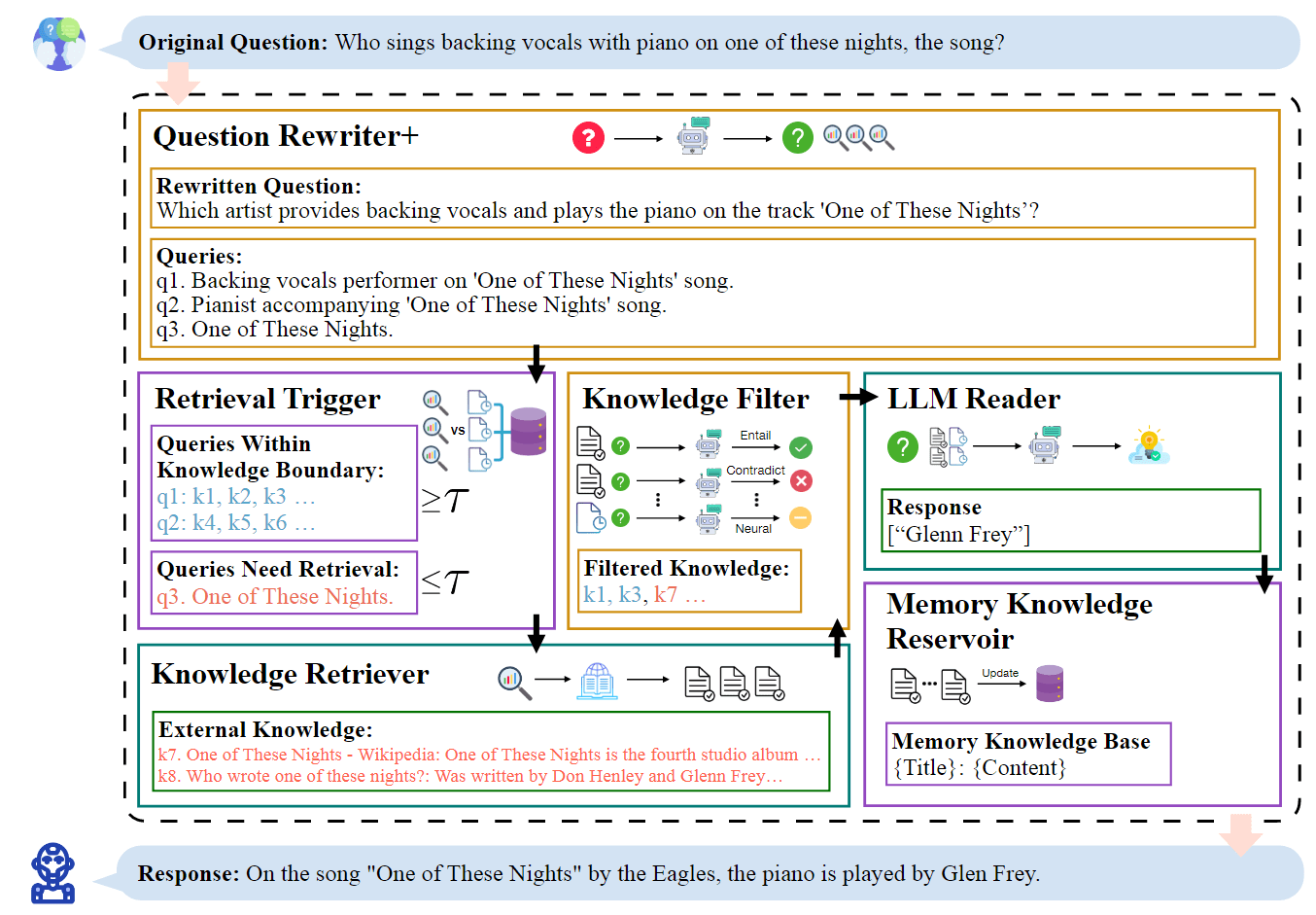
模型评估
只有选择与问题相匹配的评估方法,才能快速地发现模型选择或训练过程中出现的问题,迭代地对模型进行优化。针对分类、排序、回归、序列预测等不同类型的机器学习问题,评估指标的选择也有所不同。知道每种评估指标的精确定义、有针对性地选择合适的评估指标、根据评估指标的反馈进行模型调整,这些都是机器学习在模型评估阶段的关键问题。
首先,我们先来了解一下关于模型评估的基础概念。
【误差(error)】:学习器的预测输出与样本的真实输出之间的差异。根据产生误差的数据集,可分为:
- 训练误差(training error):又称为经验误差(empirical error),学习器在训练集上的误差。
- 测试误差(test error):学习器在测试集上的误差。
- 泛化误差(generalization error):学习器在未知新样本上的误差。
需要注意的是,上述所说的“误差”均指误差期望,排除数据集大小的影响。
【目的】:得到泛化误差小的学习器。然而,事先并不知道新样本,实际能做的是努力使经验误差最小化。但需要明确一点,即使分类错误率为 0,精度为 100% 的学习器,也不一定能够在新样本上取得好的预测结果。我们实际希望的是在新样本上能表现得很好的学习器。
为了达到这个目的,应该从训练样本中尽可能学出适用于所有潜在样本的“普遍规律”,这样才能在遇到新样本时做出正确的判别。因为,泛化误差无法测量,因此,通常我们会将测试误差近似等同于泛化误差。
过拟合与欠拟合
在模型评估与调整的过程中,我们往往会遇到“过拟合”或“欠拟合”的情况。如何有效地识别“过拟合”和“欠拟合”现象,并有针对性地进行模型调整,是不断改进机器学习模型的关键。
【过拟合】:指模型对于训练数据拟合呈过当的情况(拟合得太好了),很可能已经把训练样本自身的一些特点当作所有潜在样本都会具有的一般性质,这样就会导致泛化性能下降。反映到评估指标上,就是模型在训练集上的表现很好,但在测试集和新数据上的表现较差。
过拟合是机器学习的关键障碍,虽然各类学习算法都必然带有一些针对过拟合的措施;然而,必须认识到过拟合是无法彻底避免的,我们所能做的只是“缓解”,或者说减小其风险。
【欠拟合】:指模型在训练数据上拟合得不好,并且在测试数据上拟合得也不好。简单地说,欠拟合指的是模型在训练和预测时表现都不好的情况。主要原因在于模型的学习能力低下。

可以看出,上图(a)是欠拟合的情况,拟合的黄线没有很好地捕捉到数据的特征,不能够很好地拟合数据。图(c)则是过拟合的情况,模型过于复杂,把噪声数据的特征也学习到模型中,导致模型泛化能力下降,在后期预测过程中很容易输出错误的结果。
在一些低维的数据集上,我们可以通过数据可视化的方式来观察模型的拟合情况,但如果数据集的维度大于三维,就无法通过这种方式来进行观察。那么要怎么判断模型是否过拟合还是欠拟合呢?
吴恩达老师的深度学习课程中有讲过人类经验、训练误差以及测试误差之间的关系,课程链接 传送门,从第一周 1.8 节开始。
对于一些人类擅长的领域,例如语言、文本处理方面,人类的准确率仍然是要高于模型预测的结果,我们可以将人类经验作为模型要实现的目标,假设人类经验的错误率为 5%。此时我们训练获得一个模型的训练误差为 10%,测试误差为 11%。我们可以看到模型的训练误差对比人类经验的错误率差了 5%,也就是说该模型训练得不够好,属于欠拟合现象。然后通过一系列手段,我们再次训练模型,发现训练误差降低到了 6%,但测试误差仍然为 11%。这说明,模型在训练数据上表现得好,但在测试数据上表现得不好,属于过拟合现象。
我们可以通过人类经验、训练误差和测试误差来判断模型的训练情况,但如果不存在人类经验呢?例如一个全新的领域,没有人类经验作为参考,那么又该如何处理呢?
此时,我们仍然要比对训练误差和测试误差,如果训练误差与测试误差相差较大的话,则可以说明处于过拟合现象。若训练误差与测试误差较接近的话,则需要根据训练误差来做判断,若训练误差过大,则有可能属于欠拟合。吴恩达老师也在视频中提到,在没有人类经验作为参考,想要进一步取得突破是一件非常困难的事情。正因如此,我们在取得模型的训练误差时,仍然要想尽办法降低训练误差,因为我们不曾知道当前训练得到的误差是否已经是该模型的理论最小误差。
简单讲述了如何判断欠拟合和过拟合,再来讲讲怎么避免欠拟合以及降低过拟合风险,主要从数据以及模型这两个方面入手。
降低“欠拟合”风险的方法
【数据】:
- 获得更多的训练数据:更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。
- 添加新特征:当特征不足或者现有特征与样本标签的相关性不强时,模型容易出现欠拟合。
- 挖掘“上下文特征”、“ID 类特征”、“组合特征”等新的特征。
- 深度学习:因子分解机、梯度提升决策树、Deep-crossing 等都可以成为丰富特征的方法。
【模型】:
- 增加模型复杂度:通过增加模型的复杂度可以使模型拥有更强的拟合能力。
- 线性模型:添加高次项。
- 决策树模型:不采用剪枝手段,不限制叶节点的个数以及树的深度。
- 神经网络:增加网络层数或神经元个数。
- 减小正则化系数:针对性地减小正则化系数。
降低“过拟合”风险的方法
【数据】:
- 获得更多的训练数据:更多的样本能够让模型学习到更多更有效的特征,减小噪声的影响。
【模型】:
- 降低模型复杂度:在数据较少时,模型过于复杂是产生过拟合的主要因素,适当降低模型复杂度可以避免模型拟合过多的采样噪声。
- 神经网络:减少网络层数、神经元个数。
- 决策树:降低树的深度和叶节点的个数、进行剪枝等。
- 正则化方法:给模型的参数加上一定的正则约束,比如将权值的大小加入到损失函数中。常用的惩罚项有 l1 惩罚项和 l2 惩罚项。
- 集成学习方法:把多个模型集成在一起,来降低单一模型的过拟合风险。
【增加数据的途径】:一般来说直接增加训练数据很困难,但可以通过一定的规则来扩充训练数据。
- 图像分类问题:通过图像的平移、旋转、缩放等方式扩充数据。
- 生成式对抗网络:合成大量的新训练数据。
偏差与方差
通常我们会用过拟合、欠拟合来定性地描述模型是否很好地解决了特定的问题。从定量的角度来说,可以用模型的偏差(Bias)与方差(Variance)来描述模型的泛化性能,这称为偏差-方差分解(bias-variance decomposition),是解释学习算法泛化性能(即为什么具有这样的性能)的一种重要工具。
- 偏差:由所有采样得到的大小为 m 的训练数据集训练出的所有模型的输出的平均值和真实模型输出之间的偏差。偏差通常是由于我们对学习算法做了错误的假设所导致。例如,真实模型是某个二次函数,但我们假设模型是一次函数。由偏差带来的误差通常在训练误差上就能体现出来。简单地说,度量学习算法的期望预测与真实结果的偏离程度,即刻画了学习算法本身的拟合能力。
- 方差:由所有采样得到的大小为 m 的训练数据集训练出的所有模型的输出的方差。由方差带来的误差通常体现在测试误差相对于训练误差的增量上。简单地说,度量了同样大小的训练集的变动所导致的学习性能的变化,即刻画了数据扰动所造成的影响。
- 噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界,即刻画了学习问题本身的难度。
实际上,偏差与方差也可以用过拟合与欠拟合中所讲的“训练误差与测试误差的关系”进行解释:
- 假设模型的训练误差小,测试误差大:训练误差小,表明当前模型的偏差小;测试误差大,则说明模型在训练集和测试集上的表现差距很大,也就是说模型的方差较大,而上述这种情况属于过拟合,因此过拟合的模型一般偏差小,方差大。
- 假设模型的训练误差大,测试误差大:说明当前模型的偏差大,不管训练误差和测试误差接近与否,这种情况都属于欠拟合。
为了更好地说明偏差与方差的关系,以射击靶心作为例子。
【示例】:假设一次射击就是一个机器学习模型对一个样本进行预测。射中靶心位置代表预测准确,偏离靶心越远代表预测误差越大。我们通过 n 次采样得到 n 个大小为 m 的训练样本集合,训练出 n 个模型,对同一个样本做预测,相当于我们做了 n 次射击,射击结果如下图所示。我们最期望的结果就是左上角的结果,射击结果又准确又集中,说明模型的偏差和方差都很小;右上图虽然射击结果的中心在靶心周围,但分布比较分散,说明模型的偏差较小但方差较大;同理,左下图说明模型方差较小,偏差较大;右下图说明模型方差较大,偏差也较大。


故而,给定学习任务,为取得好的泛化性能,则需使:
- 偏差较小,即能够充分拟合数据。
- 方差较小,即使得数据扰动产生的影响小。
评估方法
考虑到篇幅问题,有关评估方法的内容放置在另一篇博客中,传送门:模型评估-评估方法
性能度量
性能度量可细分为分类问题性能度量、回归问题性能度量以及聚类问题性能度量。
- 分类问题性能度量:传送门:模型评估-性能度量(分类问题)
- 回归问题性能度量:传送门:模型评估-性能度量(回归问题)
- 聚类问题性能度量:会在后续的聚类算法中进行说明。
参考
- 《机器学习》周志华
- 《百面机器学习》