事实证明，像 BERT 这一类的预训练语言模型对 NLP 任务非常有效。但是，在训练此类模型时对计算资源的高需求阻碍了它们在实践中的应用。为了减轻大规模模型训练中的资源匮乏，作者提出了一种 Patient Knowledge Distillation（耐心的知识蒸馏）方法，将原始的大型模型（教师网络）压缩为同样有效的轻量小型模型（学生网络）。

与之前的知识蒸馏方法不同，前者仅使用教师网络最后一层的输出（《Distilling》）进行蒸馏，而本篇论文中提出的方法则是让学生网络“耐心”地从教师网络的多个中间层学习，并遵循以下两种策略来增加：

PKD-Last：从最后 K 层学习；
PKD-Skip：从每隔 K 层学习。

这两种蒸馏策略可以在教师网络的隐藏层中利用丰富的信息，并鼓励学生网络通过多层蒸馏耐心地向教师网络学习和模仿。

从经验上讲，这可以转化为多个 NLP 任务的改进结果，并且训练效率显著提高，而不会牺牲模型的准确性。

介绍

在大规模未标记数据中进行语言模型预训练，从而学习通用语言表征已被证明非常有效。ELMo、GPT 和 BERT 在许多 NLP 任务中都取得了巨大成功，例如情感分类、自然语言推理和 QA。

尽管获得了经验上的成功，但是 BERT 的计算效率仍然是一个广为人知的问题，这是因为其参数众多。例如，原始的 BERT-Base 模型具有 12 层和 1.1 亿个参数。从零开始的训练通常需要 4 到 16 块 Cloud TPU 并进行四天。即使使用任务特定的数据集对预训练模型进行微调，也可以需要几个小时才能完成一个 epoch。因此，减少此类模型的计算成本对于它们在实践中的应用至关重要，而在实践中，计算资源是有限的。

因此，作者调查了大规模预训练模型中学习参数的冗余性问题，并提出了一种新的模型压缩方法“耐心的知识蒸馏”（Patient-KD），压缩原始教师模型（例如 BERT 模型）成为轻量级的学生模型，而不会牺牲性能。在作者的方法中，教师模型输出概率对数（probability logits）并预测训练数据的标签（可以扩展到其他未标注的数据），而学生模型则从教师模型中学习以模仿教师模型的预测。

与之前的知识蒸馏方法不同，作者采用了一个“耐心的”学习机制：不再仅从教师模型的最后一层学习参数，而是鼓励学生模型从教师模型的前几层中提取知识。作者将其称为“Patient Knowledge Distillation”。该蒸馏方法的优势在于可以通过教师模型的深层结构来提炼丰富的信息，以进行多层的知识蒸馏。

作者还为蒸馏过程提出了两种不同的策略：

PKD-Last：假设原始网络的顶层包含最丰富的知识来教给学生模型，则学生模型从老师模型的最后 K 层中学习；
PKD-Skip：学生模型从教师模型的每 K 层中学习，这表明教师模型的较低层也包含重要信息，应将其传递以进行逐步提炼。

作者评估了该蒸馏方案在包括情感分类、语义相似性匹配、自然语言推理和机器阅读理解这四项 NLP 任务上的效果。在这四个任务的七个数据集上进行的实验表明，与标准知识蒸馏方法相比，PKD 方法具有更高的性能和更好的泛化能力，同时显著提高了训练效率和减少了模型的存储量，并保持与原始大模型相当的模型精度。

Patient Knowledge Distillation

在本节中，作者首先介绍用于 BERT 压缩的基础知识蒸馏方法，然后详细介绍提出的 PKD。

问题定义：，最初的大型教师模型由函数$f(X; \theta)$表示，其中 X 是模型的输入，$\theta$ 表示模型参数。知识蒸馏的目标是为小型的学生模型 $g(X;\theta’)$ 学习一组新的参数 $\theta’$，从而使学生模型获得与教师模型相似的性能，但计算成本却低得多。作者的策略是强制学生模型在定义了目标 $L_{KD}$ 的情况下，在训练数据集上模拟教师模型的输出。

蒸馏目标

在作者的设置中，将教师模型$f(X;\theta)$定义为深度双向编码器，例如 BERT。而学生模型 $g(X;\theta’)$ 则为具有较少层的轻量级模型。简单起见，作者使用 BERT_k 表示具有 k 层 Transformer 的模型，BERT-Base 和 BERT-Large 来表示 $BERT_{12}$ 和 $BERT_{24}$。

假设 ${x_i, y_i}_{i=1}^N$ 是 N 个训练数据，其中 $x_i$ 是 BERT 的第 i 个输入实例，而 $y_i$ 则是相应的真实标签。

BERT 首先计算上下文 embedding $h_i = BERT(X_i) \in \R^d$。然后，将用于分类的 softmax 层 $\hat{y}_i = P(y_i|x_i) = softmax(Wh_i)$ 应用于 BERT 输出的 embedding，其中 W 是要学习的权重矩阵。

要应用知识蒸馏，首先需要训练教师模型，例如训练一个 12 层 BERT-Base 作为教师模型，学习的参数表示为：

$$
\hat{\theta}^{t}=\arg \min {\theta} \sum{i \in[N]} L_{C E}^{t}\left(\mathbf{x}{i}, \mathbf{y}{i} ;\left[\theta_{\mathrm{BERT}_{12}}, \mathbf{W}\right]\right)
$$

其中上标 t 表示教师模型中的参数，[N] 表示集合{1, 2, …, N}，$L_{CE}^t$ 表示教师模型训练的交叉熵损失，$\theta_{BERT_{12}}$ 表示 BERT12 的参数。

任何给定输入$x_i$的输出概率可以表示为：

$$
\begin{aligned}
\hat{\mathbf{y}}{i} &=P^{t}\left(\mathbf{y}{i} | \mathbf{x}{i}\right)=\operatorname{softmax}\left(\frac{\mathbf{W} \mathbf{h}{i}}{T}\right) \
&=\operatorname{softmax}\left(\frac{\mathbf{W} \cdot \operatorname{BERT}{12}\left(\mathbf{x}{i} ; \hat{\theta}^{t}\right)}{T}\right)
\end{aligned}
$$

其中 $P^t(\cdot|\cdot)$ 表示从教师模型输出的概率，$\hat{y}_i$ 被固定为软标签，T 是知识蒸馏中使用的温度参数，它控制对教师模型的软预测的依赖程度。T 值越高，各个类别的概率分布就越多样化。类似地，让 $\theta^s$ 表示为学生模型要学习的参数，$P^s(\cdot|\cdot)$ 表示从学生模型输出的相应概率。因此，教师模型的预测和学生模型的预测之间的距离可以定义为：

$$
\begin{aligned}
L_{D S}=-\sum_{i \in[N]} \sum_{c \in C}\left[P^{t}\left(\mathbf{y}{i}=c | \mathbf{x}{i} ; \hat{\theta}^{t}\right)\right. \cdot
\left.\log P^{s}\left(\mathbf{y}{i}=c | \mathbf{x}{i} ; \theta^{s}\right)\right]
\end{aligned}
$$

其中，c 是类别标签，C 是类别标签的集合。

除了鼓励学生模型模仿老师模型的行为外，我们还可以针对目标任务对学生模型进行微调，其中特定目标的交叉熵损失包括在模型训练中。

$$
\begin{aligned}
L_{C E}^{s}=-\sum_{i \in[N]} \sum_{c \in C}\left[\mathbb{1}\left[\mathbf{y}{i}\right.\right.&=c] \cdot
\left.\log P^{s}\left(\mathbf{y}{i}=c | \mathbf{x}_{i} ; \theta^{s}\right)\right]
\end{aligned}
$$

因此，知识蒸馏的最终目标函数可以表示为：

$$
L_{K D}=(1-\alpha) L_{C E}^{s}+\alpha L_{D S} \quad (5)
$$

其中 $\alpha$ 是平衡交叉熵损失和蒸馏损失重要性的超参数。

模型压缩的耐心教师模型

使用真实标记和来自教师模型最后一层的软预测的加权组合，学生模型可以获得与训练集上的教师模型相当的性能。但是，随着 epoch 数量的增加，通过这种原始 KD 框架学习的学生模型很快就达到了测试集的饱和度（请参见第 4 节中的图 2）。

一种假设是：在知识蒸馏过程中过度拟合可能会导致泛化不良。为了缓解这个问题，作者提出了一种“耐心的”师生机制，以从教师模型的中间层中提取知识，而不是强迫学生模型仅从最后一层的 logits 中学习。

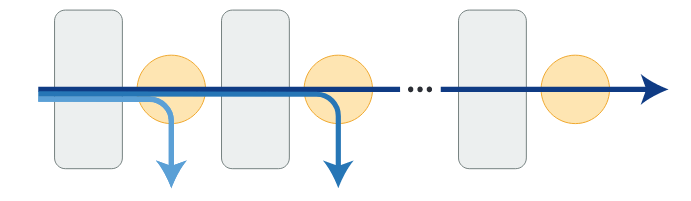
具体来说，作者研究了 PKD-Last（图 1 右）和 PKD-Skip（图 1 左）策略。

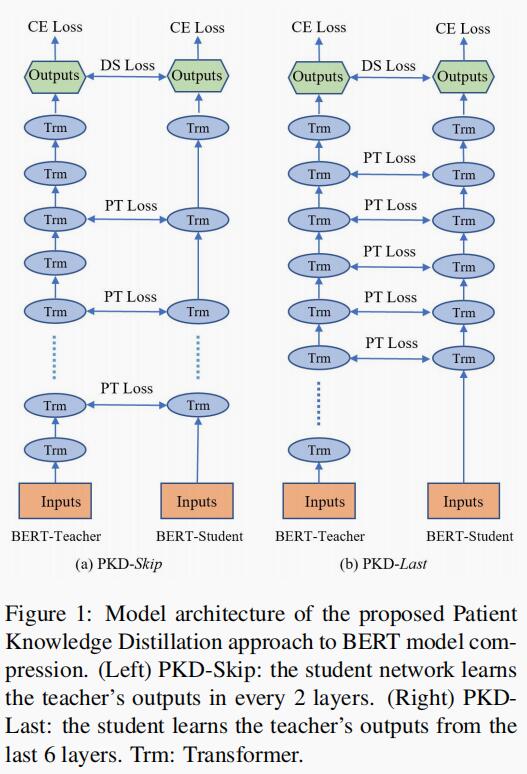
图 1 左侧为 PKD-Skip 策略，学生模型每两层学习一次教师模型的输出；图 1 右侧为 PKD-Last 策略，学生模型从最后 6 层学习教师模型的输出。其中 Trm 为 Transformer 的缩写。

从所有 token 的隐状态上进行学习是一件昂贵的计算工作，并且可能会引入噪声。在原始的 BERT 实现代码中，仅通过使用最后一层的 [CLS] token 的输出来执行预测。在一些 BERT 变体中，例如 SDNet，将所有层的 [CLS] 嵌入进行加权求平均。

通过，可以基于 $h_{final} = \sum_{j\in[k]} w_jh_j$，其中 $w_j$ 可以是学习的参数，也可以是预定义的超参数。$h_j$ 是来自隐藏层 j 的 [CLS] embedding，而 k 是隐藏层的数量。由此推论，如果学生模型可以针对任何给定输入，从教师模型的中间层的 [CLS] 表征中学习，则学生模型具有获得类似于教师模型的泛化能力的潜力。在 PKD 框架中，也采用相同的做法，训练学生模型只模仿教师模型中间层的 [CLS] token 表征。对于输入$x_i$，所有层的 [CLS] token 的输出表示为：

$$
\mathbf{h}{i}=\left[\mathbf{h}{i, 1}, \mathbf{h}{i, 2}, \ldots, \mathbf{h}{i, k}\right]=\operatorname{BERT}{k}\left(\mathbf{x}{i}\right) \in \mathbb{R}^{k \times d} \quad (6)
$$

$I_{pt}$ 表示从教师模型进行知识蒸馏的中间层集合。以从 BERT12 蒸馏到 BERT6 为例，对于 PKD-Skip 策略，$I_{pt} = {2, 4, 6, 8, 10}$，而 PKD-Last 策略，$I_{pt} = {7, 8, 9, 10, 11}$。需要注意的是，两种情况下 k = 5，因为省略了最后一层的输出，因为其隐状态已连接到 softmax 层，该层已包含在等式 5 定义的知识蒸馏损失中。通常，对于具有 n 层的 BERT 学生模型，k 始终等于 n - 1。

由教师模型引入的额外训练损失定义为归一化隐状态之间的均方损失：

$$
L_{P T}=\sum_{i=1}^{N} \sum_{j=1}^{M}\left|\frac{\mathbf{h}{i, j}^{s}}{\left|\mathbf{h}{i, j}^{s}\right|{2}}-\frac{\mathbf{h}{i, I_{p t}(j)}^{t}}{\left|\mathbf{h}{i, I{p t}(j)}^{t}\right|{2}}\right|{2}^{2}
$$

其中 M 表示学生模型中的层数，N 表示训练数据数，h 中的上标 s 和 t 分别表示学生模型和教师模型。结合第 3.1 节中介绍的知识蒸馏损失，最终目标函数可以表示为：

$$
L_{P K D}=(1-\alpha) L_{C E}^{s}+\alpha L_{D S}+\beta L_{P T}
$$

其中$\beta$是另一个超参数，它权衡了中间层蒸馏特征的重要性。

实验

在本节中，作者将提出的 PKD 方法应用于四个不同的 NLP 任务的实验。以下小节提供了有关数据集和实验结果的详细信息。

数据集

作者使用了 SST-2、MRPC、QQP、MNLI-m、MNLI-mm、QNLI 和 RTE 数据集。

基线和训练细节

对于在 GLUE 基准上进行的实验，由于所有任务都可以视为句子（或句子对）分类，因此作者在原始 BERT 中使用相同的结构，并独立地对每个任务进行微调。

作者将 BERT-Base（表示为 BERT12）微调为教师模型，以独立计算每个任务的软标签，其中预训练的模型权重是从 Google 官方的 BERT 的 repo 获得。然后使用 3 层和 6 层的 Transformer 作为学生模型（表示为 BERT3 和 BERT 6）。作者使用来自预训练的 BERT-Base 的前 K 个参数层来初始化 BERTk，其中 $k\in{3,6}$。为了验证提出的方法的有效性，作者首先对每个任务进行直接微调，而无需使用任务软标签。

为了减少超参数搜索空间，对于所有试验，作者将最终 softmax 层中的隐藏单元数量固定为 768，批量大小固定为 32，并将 epoch 固定为 4，学习率来自 {5e-5, 2e-5, 1e-5}。为每个设置选择具有最佳验证将高度的模型。

除了直接微调外，作者还通过优化等式 5 中的目标函数，在所有任务上进一步实现了基础的 KD 方法。作者将温度参数 T 设置为 {5, 10, 20}，$\alpha = {0.2, 0.5, 0.7}$，并在 T、$\alpha$ 和学习率上进行网络搜索，以选择具有最佳验证精度的模型。

对于作者提出的 PKD 方法，在{10, 100, 500, 1000} 的所有任务上对 $\beta$ 进行额外的搜索。由于需要为 PKD 学习的超参数太多，因此将 $\alpha$ 和 T 固定为基础 KD 实验中获得最佳性能的值，仅搜索 $\beta$ 和学习率。

实验结果

作者将模型预测结果提交给官方 GLUE 评估服务器以获取测试数据的结果，结果总结在表 1 中。

与直接 fine-tuning 和基础 KD 相比，使用 PKD 的 BERT3 和 BERT6 模型在除 MRPC 之外的几乎所有任务上均表现最佳。

此外，在 7 项任务中的 5 项中，使用 PKD 的 BERT6 层学生模型与原始的 BERT-Base 模型取得了相似的成绩，这证明了 PKD 方法的有效性。有趣的是，所有这 5 个任务的训练样本均超过 60k，这表明当有大量训练数据时，作者提出的 PKD 方法往往表现更好。

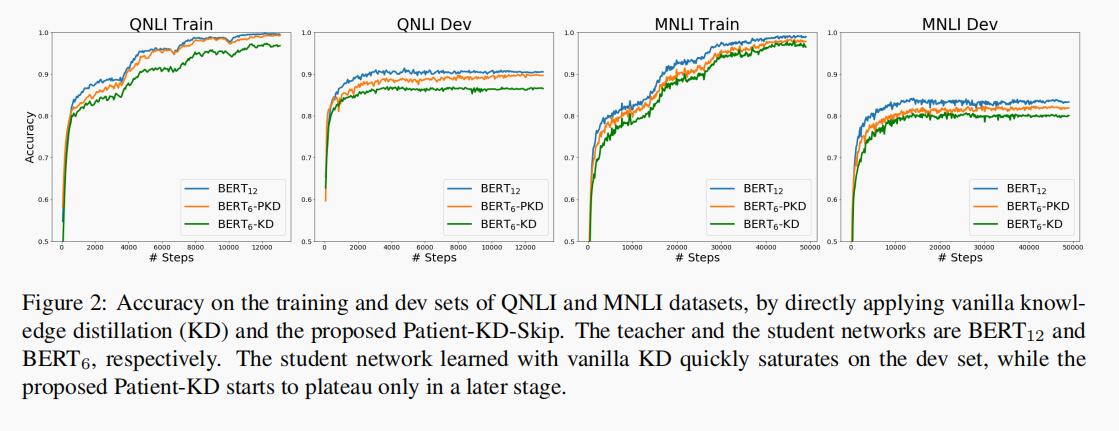
QNLI 和 MNLI 数据集的学习曲线如图 2 所示。使用基础 KD 学习的学生模型在开发集上迅速饱和，而提出的 PKD 则继续向教师模型学习并提高了准确性。

对于 MRPC 数据集，基础 KD 优于 PKD 的一种假设是：缺乏足够的训练数据可能会导致对验证集的过拟合。为了进一步研究，作者重复了 3 次试验，并在验证集上计算平均精度。作者观察到，微调和基础 KD 的平均验证精度分别为 82.23% 和 82.84%。PKD 具有较高的平均验证精度，达到 83.46%，这表明由于少量的训练数据，PKD 方法与 MRPC 的验证集有些过拟合。在表 5 中，RTE 上教师模型和学生模型之间的表现差距也可以观察到，表 5 中的训练数据也很少。

作者进一步研究了两种不同的 PKD 策略：PKD-Last 和 PKD-Skip。表 2 总结了 GLUE 基准测试中两种 PKD 变体的结果（以 BERT6 作为学生模型）。

尽管两种策略均优于基础的 KD baseline（见表 1），但 PKD-Skip 的性能略好于 PKD-Last。据推测，这可能是由于以下事实：在每 K 层上提取信息会捕获从底层到高层的更丰富语义的更多不同表征，而专注于最后 K 层往往会捕获相对同质的语义信息。

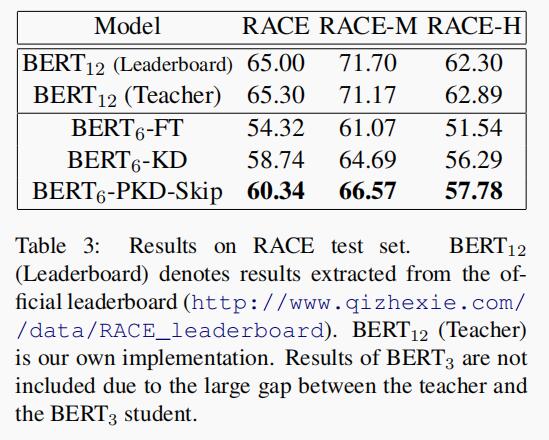
表 3 中报告了 RACE 的结果，该结果表明基础 KD 方法优于直接微调 4.42%，而作者提出的 PKD 比基础的 KD 方法提升了 1.6%，这再次证明了 PKD 的有效性。

模型效率分析

表 4 总结了参数统计信息和推断时间。所有模型都具有相同的嵌入层和 2400 万个参数，这些参数将 3 万单词的词汇表映射到 768 维向量，这分别从 BERT6 和 BERT3 节省了 1.64 和 2.4 倍的机器内存。

为了测试推理速度，作者对来自 QNLI 训练集的 105000 个样本进行了实验。推理是在单个 Titan RTX GPU 上执行的，批处理大小设置为 128，最大序列长度设置为 128，并且激活了 FP16。

与 Transformer 层相比，embedding 层的推断时间可以忽略不计。表 4 中的结果表明，提出的 PKD 方法几乎实现了线性的加速，分别是 BERT6 和 BERT3 的 1.94 和 3.73 倍。

更好的老师会有帮助吗？

为了评估 PKD 框架中教师模型的有效性，作者进行了额外的实验，来测量 BERT-Base 教师模型和 BERT-Large 教师模型之间的模型压缩差异。

BERT-Large 中的每个 Transformer 层都有 1260 万个参数，比 BERT-Base 中使用的 Transformer 层大得多。对于具有 6 层的压缩 BERT 模型，BERT6-Base 仅具有 6700 万个参数，而 BERT6-Large 具有 1.084 亿个参数。由于 [CLS] token 嵌入的大小在 BERT-Large 和 BERT-Base 之间是不同的，因此当 BERT-Large 被用作教师模型时，无法直接计算 BERT6-Base 的 patient teacher 损失（等式 7）。因此，在教师模型为 BERT-Large 而学生模型是 BERT6-Base 的情况下，作者仅在基础 KD 设置下进行实验。

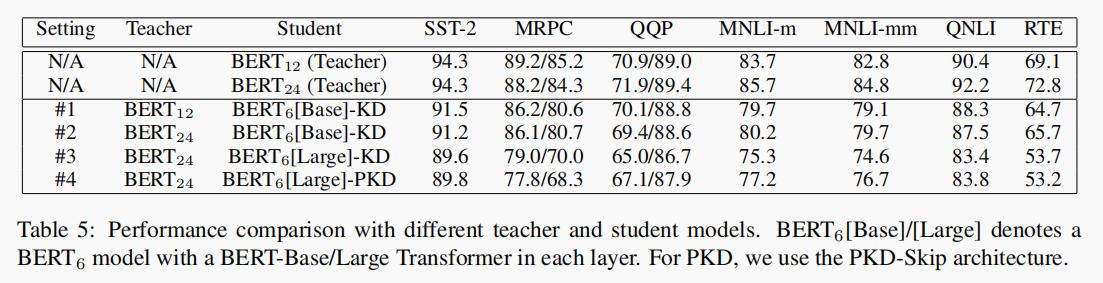
结果总结在表 5 中，当教师模型从 BERT12 更改为 BERT24（即设置 #1 和 #2）时，学生模型的表现之间并没有太大差异。据推测，从更大的教师模型那里提取知识需要更大的训练数据集，因此在 MNLI-m 和 MNLI-mm 上可获得更好的结果。

有趣的是，在将设置 #1 和 #3 进行比较时，即使使用了更好的教师模型，BERT5-Large 的性能也比 BERT6-Base 差得多。这背后的一种猜测是 BERT6-Large 模型的压缩比为 4：1（24：6），大于 BERT6-Base 模型的压缩比 2：1（12：6）。较高的压缩比使学生模型学习教师模型中重要的权重更具挑战。

比较设置 #2 和 #3 时，可以发现即使使用相同的教师模型，BERT6-Large 的性能仍然比 BERT6-Base 差。据推测，这可能是由于初始化不匹配。理想情况下，应该从头开始对 BERT6-Large 和 BERT6-Base 进行预训练，并将从预训练步骤中学到的权重用于 KD 训练中的权重初始化。但是，由于从头开始训练 BERT6 的计算限制，作者仅使用 BERT12 或 BERT24 的前 6 层初始化学生模型。因此 BERT24 的前 6 层可以能无法捕获高层特征，从而导致较差的 KD 性能。

最后，比较设置 #3 和 #4，在 #4 中使用 PKD 代替了基础的 KD，可以观察到几乎所有任务的性能都有提高，这表明 PKD 是通用的，与教师模型的选择无关。