论文阅读:Self-Consistency Improves Chain of Thought Reasoning in Language Models
思维链 prompt 与预训练的大型语言模型相结合,在复杂的推理任务上取得了令人鼓舞的结果。在本文中,作者提出了一种新的解码策略,即自我一致性(self-consistency),以取代思维链 prompt 中使用的 naive 贪婪解码。它首先对不同的推理路径进行抽样,而不是只采取贪婪的推理路径,然后通过对抽样的推理路径进行边际化处理,选择最一致的答案。自我一致性利用了这样一种直觉:一个复杂的推理问题通常会有多种不同的思维方式,从而引导其唯一的正确答案。
有点类似于学生时代的考试,第一遍做题得出结果,在第二遍检查时,抛开先前的记忆重新再计算一次,看看两次的结果是否一致,如果不一致说明存在问题,那么就需要重点去思考题目的正确结果。
广泛的实证评估表明,在一系列流行的算术和常识推理基准上,自我一致性以惊人的幅度提高了思维链 prompt 的性能,包括 GSM8K(+17.9%)、SVAMP(+11.0%)、AQuA(+12.2%)、StrategyQA(+6.4%)和 ARC-challenge(+3.9%)。
不同推理路径上的自我一致性
人类的一个突出方面是,人们的思维方式不同。作者很自然地认为,在需要深思熟虑的任务中,很可能有几种方法来解决这个问题,这样的过程可以通过语言模型的解码器的抽样在语言模型中模拟出来。
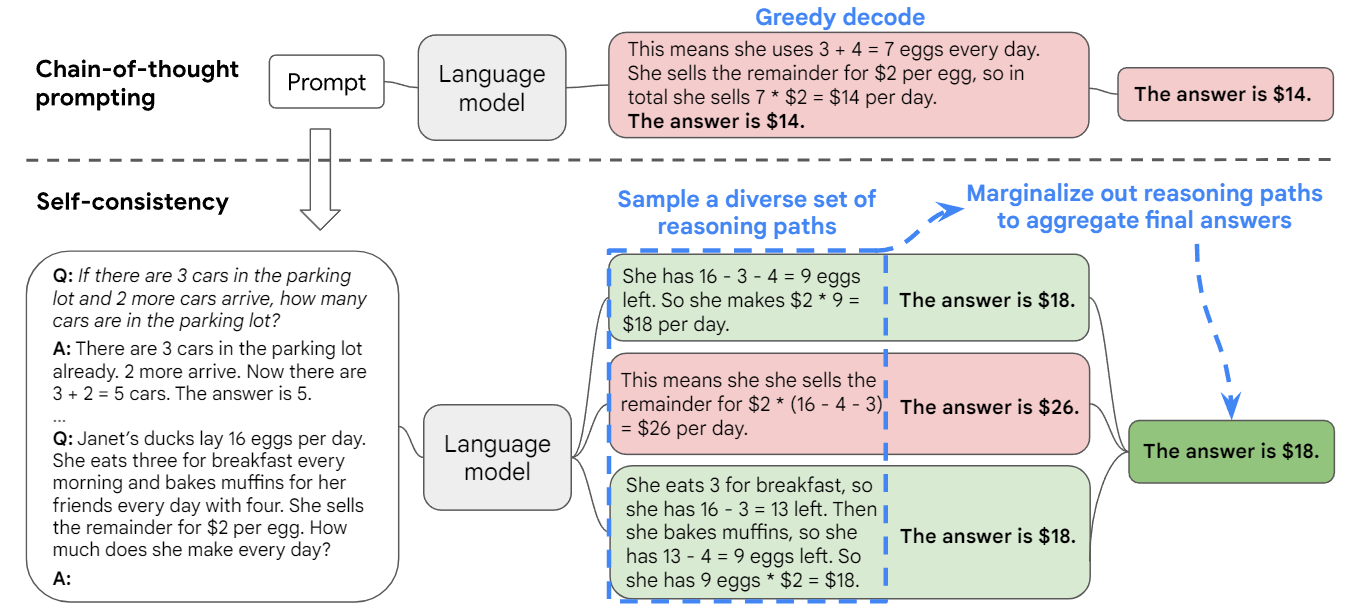
图 1:自我一致性方法包含三个步骤:(1)使用思维链(CoT)prompt 语言模型;(2)通过从语言模型的解码器中取样来取代 CoT prompt 中的“贪婪解码”,从而产生一个多样化的推理路径集;以及(3)通过在最终答案集中选择最一致的答案来边际化出推理路径并进行汇总。
例如,如图 1 所示,一个模型可以对一个数学问题产生几个貌似合理的回答,而这些回答都得出了相同的正确答案(输出 1 和 3)。由于语言模型不是完美的推理者,模型也可能产生一个不正确的推理路径或在某个推理步骤中犯错(例如在输出 2 中),但这样的解决方案不太可能得出相同的答案。也就是说,假设正确的推理过程,即使它们是多样化的,也往往比不正确的过程在最终答案上有更大的一致性。作者利用这一直觉,提出了以下自我一致性方法。
- 首先,用一组人工书写的思维链示例来 prompt 语言模型。
- 接着,从语言模型的解码器中抽出一组候选输出,生成一组多样化的候选推理路径。自我一致性与大多数现有的采样算法兼容,包括:
- temperature 采样。
- top-k 采样。
- nucleus(核)采样。
- 最后,通过将抽样的推理路径边际化(marginalization)来汇总答案,并在生成的答案中选择最一致的答案。
更详细地说,假设生成的答案 $a_i$ 来自一个固定的答案集,$a_i \in A$。给定一个 prompt 和一个问题,自我一致性引入了一个额外的潜在变量 $r_i$,表示第 i 个输出的推理路径的 token 序列,生成推理路径 $r_i$ 用来生成最终答案 $a_i$。
问题:为什么需要一个固定的答案集?
回答:因为需要借助自我一致性来汇总最后的答案,相当于集成学习中多个分类器对分类结果的投票,如果答案五花八门则难以投票出结果,所以答案是一个固定的集合,这对于自我一致性的使用范围来说是一个限制。
考虑图 1 中的输出 3:前几句“She eats 3 for breakfast … So she has 9 eggs * $2 = $18.” 构成 $r_i$,而最后一句中的答案 18,“The answer is $18” 被解析为 $a_i$。在从模型的解码器中抽取多个 $(r_i, a_i)$ 后,自我一致性通过对 $a_i$ 进行多数投票,即 $arg max_a \sum_{i=1}^m I(a_i = a)$,或如所定义的那样,在最终的答案集中选择最“一致”的答案。
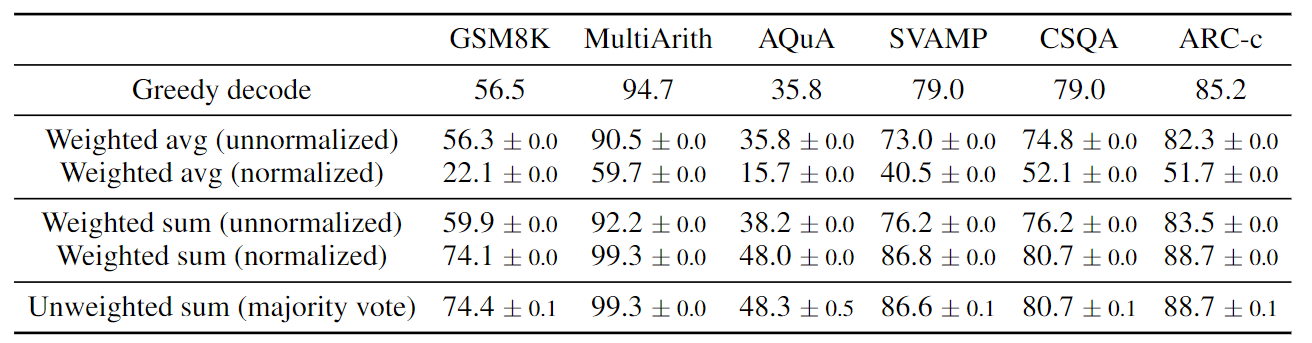
表 1:PaLM-540B 上不同答案汇总策略的准确性比较。
在表 1 中,展示了通过使用不同的答案汇总策略对一组推理任务的测试准确性。除了多数票,还可以在汇总答案时用 $P(r_i, a_i | prompt, question)$ 对每个 $(r_i, a_i)$ 进行加权。注意,计算 $P(r_i, a_i | prompt, question)$ 时,可以取给定 (prompt, question) 的模型产生 $(r_i, a_i)$ 的非归一化概率,或者通过输出长度将条件概率归一化(Brown 等人,2020),即:
$$
P(r_i, a_i | prompt, question) = exp^{\frac{1}{K} \sum_{k=1}^K log P(t_k | prompt, question, t_1, \ldots, t_{k - 1})}, \tag{1}
$$
其中 $logP(t_k | prompt, question, t_1, \ldots, t_{k-1})$ 是在 $(r_i, a_i)$ 中产生第 k 个 token $t_k$ 的对数概率,以先前的 tokens 为条件,K 是 $(r_i, a_i)$ 中 tokens 的总数。
在表 1 中,采取“unweighted sum”(非加权总和),即直接对 $a_i$ 进行多数投票,与使用“normalized weighted sum”(归一化加权总和)进行汇总的准确性非常相似。作者仔细观察了模型的输出概率,发现这是因为对于每一个 $(r_i, a_i)$,归一化的条件概率 $P(r_i, a_i | prompt, question)$ 都相当接近,也就是说,语言模型将这些生成视为“相似的可能性”(这也意味着语言模型没有得到很好的校准,因此不能很好地区分正确的解决方案和错误的解决方案,这也解释了为什么在以前的工作中要训练额外的重排器来更好地判断解决方案的质量(Cobbe 等人,2021;Thopilan 等人,2022))。
此外,当汇总答案时,表 1 中的结果显示,归一化的加权和(即公式 1)与未归一化的对应方相比,产生了更高的准确性。为了完整起见,在表 1 中还报告了采取 “加权平均 “的结果,即每个 a 得到的分数是其加权和除以 $\sum_{i=1}^m I(a_i = a)$,这导致了更糟糕的性能。
自我一致性在开放式文本生成和具有固定答案的最佳文本生成之间探索了一个有趣的空间。推理任务通常有固定的答案,也就是为什么研究人员普遍考虑贪婪的解码方法。然而,作者发现,即使所需的答案是固定的,在推理过程中引入多样性也是非常有益的;因此,利用采样,正如通常用于开放式文本生成(Radford等人,2019;Brown等人,2020;Thopilan等人,2022),以实现这一目标。人们应该注意到,自我一致性只适用于最终答案来自固定答案集的问题,但原则上,如果能在多轮生成之间定义一个良好的一致性指标,例如,两个答案是否一致或相互矛盾,这种方法可以扩展到开放式文本生成问题。
相关实验
在一系列的推理基准上将所提出的自我一致性方法与现有的方法进行比较。作者发现,对于所考虑的每一个语言模型,自我一致性都能稳健地提高推理的准确性,并且在各模型规模上都有提升。
关于实验的具体设置,读者可自行去阅读论文,其中包含测试的 prompt、解码时的参数设置,例如温度、top-p 等等。
当思维链伤害到性能时,自我一致性会有所帮助
Ye & Durrett(2022)表明,与标准的 prompt 相比,有时思维链 prompt 可能会伤害到 few-shot 的 ICL 表现。在这里,用自我一致性进行了一项研究,看看它是否可以帮助填补这一空白,在一组常见的 NLP 任务中,包括:
- 闭卷答题:BoolQ、HotPotQA
- 自然语言推理:e-SNLI、ANLI 和 RTE
超过 PaLM-540B 的结果显示在表 5 中。对于某些任务(如 ANLI-R1、e-SNLI、RTE),与标准 prompt 相比,添加思维链确实会损害性能(Brown 等人,2020),但自我一致性能够稳健地提升性能,并超过标准 prompt,使其成为在常见 NLP 任务的 few-shot ICL 中使用的可靠方法。

表 5:比较标准/CoT prompt 与常见 NLP 任务的自我一致性。
与其他现有方法相比
作者进行了一系列额外的研究,结果表明自我一致性明显优于现有的方法,包括采样和排序、beam search 和基于集成的方法。
与采样和排序相比
一种常用的提高生成质量的方法是采样和排序,即从解码器中抽出多个序列,然后根据每个序列的对数概率进行排序(Adiwardana 等人,2020)。作者在 GPT-3 code-davinci-001 上比较了自我一致性与采样和排序,通过从解码器中抽出与自我一致性相同数量的序列,并从排名靠前的序列中获取最终答案。
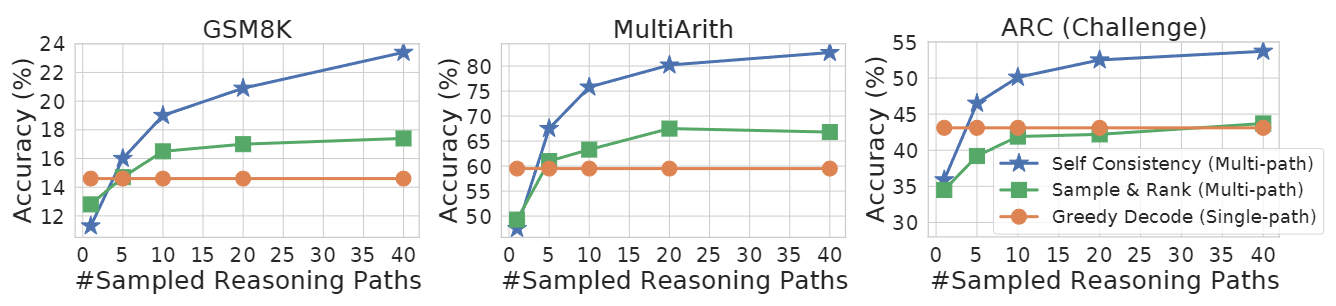
图 3:在相同数量的样本中,自我一致性明显优于采样和排序。
结果显示在图 3 中。虽然采样和排序确实提高了额外采样序列和排名的准确性,但与自我一致性相比,其增益要小得多。
和 beam search 相比
在表 6 中,作者对 UL2-20B 模型的自我一致性与 beam search 解码进行了比较。为了进行公平比较,报告了相同 beam 数量和推理路径下的精度。

表 6:UL2-20B 模型与 beam search 解码的自我一致性比较。
在这两项任务中,自我一致性都明显优于 beam search。需要注意的是,自我一致性也可以采用 beam search 对每条推理路径进行解码(结果显示为“使用 beam search 的自我一致性”),但其性能比使用采样的自我一致性更差。原因是 beam search 产生的输出多样性较低,而在自我一致性中,推理路径的多样性是获得更好性能的关键。
与基于集合的方法比较
作者还将自我一致性方法与基于集合的方法进行了比较,以便进行 few-shot learning。特别是,考虑通过以下方法进行集合:
- prompt 顺序置换:将 prompt 中的示例随机置换 40 次,以减轻模型对 prompt 顺序的敏感性
- 多组 prompt:手动编写 3 组不同的 prompt。
将两种方法中贪婪解码所得答案的多数票作为一个集合。

表 7:在 LaMDA-137B 上,自我一致性优于 prompt-order 和 multi-prompt 集成。
表 7 显示,与自我一致性相比,现有的基于集合的方法获得的增益要小得多。此外,需要注意的是,自我一致性不同于典型的模型集合方法,即训练多个模型并将其输出汇总。自我一致性更像是在单个语言模型基础上的“自组装”
总结和讨论
引入了一种简单而有效的方法,称为自我一致性,并观察到它在一系列算术和常识推理任务中,在四个不同规模的大型语言模型中明显提高了准确性。除了准确性的提高,自我一致性也有助于在用语言模型进行推理任务时收集理由,并提供不确定性估计和改进语言模型输出的校准。
自我一致性的一个限制是它会产生更多的计算成本。在实践中,人们可以尝试少量的路径(如 5 条或 10 条)作为起点,以实现大部分的收益,同时不产生太多的成本,因为在大多数情况下,性能很快就饱和了,见下图 2。

图 2:在算术和常识推理任务中,自我一致性(蓝色)比带有贪婪解码(橙色)的 CoT 提示(LaMDA-137B)显著提高了推理的准确性。对更多不同推理路径进行采样可持续提高推理准确率。
在这我们可以考虑使用一些部署框架,例如 vLLM。该框架提出了 PagedAttention,灵感来自于操作系统虚拟内存和分页思想。与传统的注意力算法不同,PagedAttention 允许在非连续的内存空间中存储连续的 key 和 value。具体来说,PagedAttention 将每个序列的 KV cache 划分为 blocks,每个 block 包含固定数量 token 的键和值。在注意力计算时,PagedAttention 内核可以更高效的识别和获取这些 blocks。
PagedAttention 在 parallel sampling 和 beam search 生成时还有额外的优势:共享 prompt 部分的内存,这可以提升 2.2x 的速度和降低 55% 的内存使用。
我们可以直接使用官方提供的 fastapi 部署服务方式,地址:https://github.com/vllm-project/vllm/blob/main/vllm/entrypoints/api_server.py。在请求体内添加参数 n,n 即为输出的结果数量。关于 sampling_params 可参考 https://github.com/vllm-project/vllm/blob/main/vllm/sampling_params.py。
此外,作者观察到,语言模型有时会产生不正确或无意义的推理路径(例如,表 4 中的 StrategyQA 示例,两个人口数并不完全正确),需要进一步的工作来更好地支持模型的推理生成。
在这可以结合 RAG 以及 Tool Use Agent,来增强模型推理路径的生成,或者直接提供更好的推理路径。
另外,如何选择“最一致”的答案也有很多方式,例如在开放式闲聊场景中,使用奖励模型来评分是一个不错的方式,让模型生成多条回复,通过奖励模型打分,挑选分数最高的回复。