AGNES

AGNES（AGglomerative NESting 的简写）是一种采用自底向上聚合策略的层次聚类算法。

【工作过程】：

1. 先将数据集中的每个样本看作一个初始聚类簇；
2. 然后在算法运行的每一步中找出距离最近的两个聚类簇进行合并；
3. 步骤（2）不断重复，直至达到预设的聚类簇的个数。

【关键】：如何计算聚类簇之间的距离。

实际上，每个簇是一个样本集合，因此，只需采用关于集合的某种距离即可。
$$
\text{最小距离：}d_{min}(C_i, C_j) = min_{x\in C_i,z\in C_j}dist(x,z)
$$

$$
\text{最大距离：}d_{max}(C_i, C_j) = max_{x\in C_i,z\in C_j}dist(x,z)
$$

$$
\text{平均距离：}d_{avg}(C_i, C_j) = \frac{1}{|C_i||C_j|}\sum_{x\in C_i}\sum_{z\in C_j}dist(x,z)
$$

显然，最小距离由两个簇的最近样本决定，最大距离由两个簇的最远样本决定，而平均距离则由两个簇的所有样本共同决定。

当聚类簇距离为

• $d_{min}$：AGNES 算法被称为“单链接”（single-linkage）；
• $d_{max}$：AGNES 算法被称为“全链接”（complete-linkage）；
• $d_{avg}$：AGNES 算法被称为“均链接”（average-linkage）。

此外，豪斯多夫距离（Hausdorff distance）也可用于集合间的距离计算。关于豪斯多夫距离的介绍可参考这篇博文豪斯多夫距离

【算法描述】：

• 输入：样本集 $D = {x_1, x_2, \cdots, x_n}$;聚类簇距离度量函数 dist；聚类簇数 k。
• 输出：簇划分 $C = {C_1, C_2, \cdots, C_k}$。
• 过程：

1. 为每个样本创建一个簇；
2. 计算距离矩阵；
3. 开始合并簇过程，初始化聚类簇个数 q = n：
   • 每次从距离矩阵中找出距离最近的两个聚类簇 $C_i$ 和 $C_j$，i < j；
   • 合并这两个簇（优先合并到下标较小的簇 $C_i$）$C_i = C_i \bigcup C_j$；
   • 将聚类簇重新编号（合并到下标较小的簇可以减少重编号的次数）；
   • 删除距离矩阵的第 j 行与第 j 列；
   • 计算合并后的簇 $C_i$ 与剩余其他簇之间的距离，并更新距离矩阵。
   • q = q - 1。
   • 直到 q == k 时，退出循环。
4. 返回簇划分。

案例说明

id	density	sugar content	id	density	sugar content	id	density	sugar content
1	0.697	0.460	11	0.245	0.057	21	0.748	0.232
2	0.774	0.376	12	0.343	0.099	22	0.714	0.346
3	0.634	0.264	13	0.639	0.161	23	0.483	0.312
4	0.608	0.318	14	0.657	0.198	24	0.478	0.437
5	0.556	0.215	15	0.360	0.370	25	0.525	0.369
6	0.403	0.237	16	0.593	0.042	26	0.751	0.489
7	0.481	0.149	17	0.719	0.103	27	0.532	0.472
8	0.437	0.211	18	0.359	0.188	28	0.473	0.376
9	0.666	0.091	19	0.339	0.241	29	0.725	0.445
10	0.243	0.267	20	0.282	0.257	30	0.446	0.459

以上述数据集（《机器学习》西瓜集 4.0）为例，令 AGNES 算法一直执行到所有样本出现在同一个簇中，即 k = 1，即可得到下图所示的“树状图”（dendrogram），其中每层链接一组聚类簇。

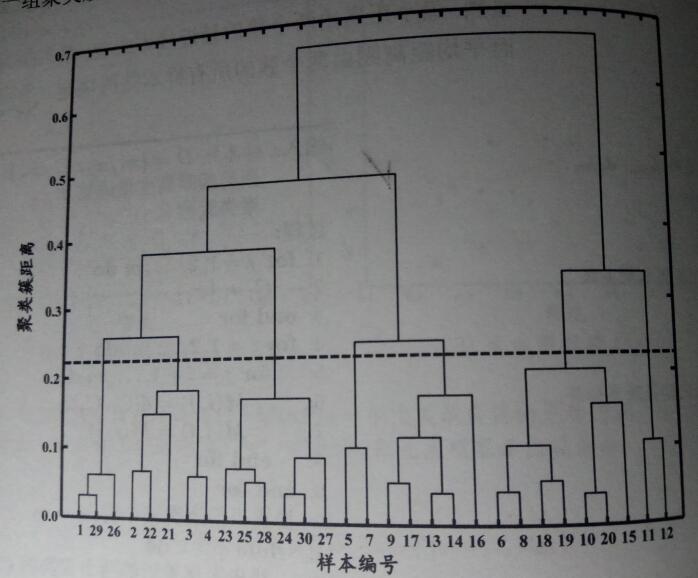
观测树状图的合并结果，可以发现该合并结果是 AGNES 算法以“最大距离”作为距离度量标准进行合并。此外，在树状图的特定层次上进行分割，则可得到相应的簇划分结果。例如，以图中所示虚线分割树状图，将得到包含 7 个聚类簇的结果。

• C1 = {x1, x26, x29}；
• C2 = {x2, x3, x4, x21, x22}；
• C3 = {x23, x24, x25, x27, x28, x30}；
• C4 = {x5, x7}；
• C5 = {x9, x13, x14, x16, 17}；
• C6 = {x6, x8, x10, x5, x18, x19, x20}；
• C7 = {x11, x12}。

将分割层逐步提升，则可得到聚类簇逐渐减小的聚类结果。下图显示 AGNES 算法产生 7 至 4 个聚类簇的划分结果。

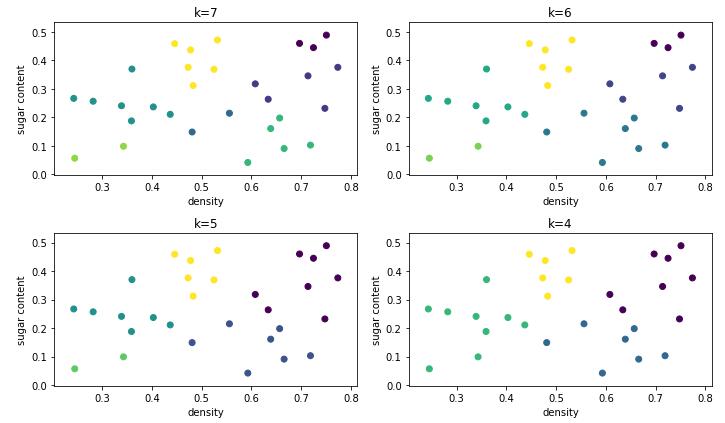
代码实现

首先实现距离计算函数。

def get_dist(XA, XB, type='min'):
    if len(XA.shape) == 1:
        XA = np.array([XA])
    if len(XB.shape) == 1:
        XB = np.array([XB])
    dist = 0
    if type == 'min':
        dist = cdist(XA, XB, 'euclidean').min()
    elif type == 'max':
        dist = cdist(XA, XB, 'euclidean').max()
    else:
        dist = cdist(XA, XB, 'euclidean').sum() / XA.shape[0] / XB.shape[0]
    return dist

然后编写 AGNES 函数的实体：

• 函数定义

def AGNES(dataset, k, dist_method='avg'):

• 初始化所需变量

# 获取样本集长度
length = dataset.shape[0]
# 初始化聚类簇和距离矩阵
clusters, dist_matrix = [], np.mat(np.zeros((length, length)))

• 为每个样本分配一个聚类簇

for data in dataset:
    clusters.append(data)

• 计算距离矩阵

for i in range(length):
    for j in range(length):
        if i == j:
            dist = np.inf
        else:
            dist = get_dist(clusters[i], clusters[j], dist_method)
        dist_matrix[i, j] = dist
        dist_matrix[j, i] = dist

• 设置当前聚类簇的个数，并开始合并过程

cluster_count = length
while cluster_count > k:

• 找出距离最近的两个聚类簇

first, second = np.where(dist_matrix == dist_matrix.min())[0]

• 合并这两个聚类簇

clusters[first] = np.vstack((cluters[first], clusters[second]))

• 将聚类簇重新编号

for i in range(second + 1, cluster_count):
    clusters[i - 1] = clusters[i]
clusters.pop()

• 删除距离矩阵的第 second 行与列

dist_matrix = np.delete(dist_matrix, second, axis=0)
dist_matrix = np.delete(dist_matrix, second, axis=1)

• 重新计算距离矩阵第 first 簇与其他簇之间距离

for i in range(cluster_count - 1):
    if first == i:
        dist = np.inf
    else:
        dist = get_dist(clusters[first], clusters[i], dist_method)
    dist_matrix[first, i] = dist
    dist_matrix[i, first] = dist

• q = q - 1

cluster_count -= 1

• 返回簇划分

return clusters

【完整代码】：传送门

def AGNES(dataset, k, dist_method='avg'):
    length = dataset.shape[0]
    clusters = []
    dist_matrix = np.mat(np.zeros((length, length)))
    for data in dataset:
        clusters.append(data)
    for i in range(length):
        for j in range(length):
            if i == j:
                dist = np.inf
            else:
                dist = get_dist(clusters[i], clusters[j], dist_method)
            dist_matrix[i, j] = dist
            dist_matrix[j, i] = dist

    # 设置当前聚类簇的个数
    cluster_count = length
    
    while cluster_count > k:
        # 找出距离最近的两个聚类簇
        first, second = np.where(dist_matrix == dist_matrix.min())[0]
        
        # 合并这两个聚类簇
        clusters[first] = np.vstack((clusters[first], clusters[second]))
        
        # 重新编号聚类簇
        for i in range(second + 1, cluster_count):
            clusters[i - 1] = clusters[i]
        clusters.pop()
        
        # 删除距离矩阵的第 second 行与列
        dist_matrix = np.delete(dist_matrix, second, axis=0)
        dist_matrix = np.delete(dist_matrix, second, axis=1)        
        
        # 重新计算距离矩阵第 first 簇与其他簇之间距离
        for i in range(cluster_count - 1):
            if first == i:
                dist = np.inf
            else:
                dist = get_dist(clusters[first], clusters[i], dist_method)
            dist_matrix[first, i] = dist
            dist_matrix[i, first] = dist
        cluster_count -= 1
    return clusters

参考

• 《机器学习》周志华
• 豪斯多夫距离：https://blog.csdn.net/swallowwd/article/details/81538726