博客的数学公式显示有些许问题，更佳的阅读体验请参阅 https://www.wolai.com/voY74vy53rt6bwrMBzEDDU 。

Flash Attention 是一种新型的注意力机制，旨在解决传统 Transformer 模型在处理长序列数据时面临的计算和内存效率问题。它通过一系列创新的技术优化，显著提高了注意力机制的计算速度和内存使用效率，同时保持了精确的结果，不依赖于近似计算。

背景&动机

当输入序列较长时，Transformer 的计算过程缓慢且耗费内存，这是因为 self-attention 的时间和内存复杂度会随着序列长度的增加而呈二次增长。标准 Attention 计算的中间结果 S, P（见下文）通常需要通过 HBM 进行存取，两者所需内存空间复杂度为$O(N^2)$。

$$
self-attention(x) = softmax(\frac{Q K^T}{\sqrt{d}})\cdot V
$$

$$
S = \frac{Q K^T}{\sqrt{d}}, \quad P = softmax(S)
$$

在不考虑 batch size 的前提下，令 N 表示序列长度，d 表示注意力头维度（隐藏层维度 / 注意力头数）。那么，Q、K 和 V 矩阵的 shape 为 [N, d]，S 和 P 的 shape 为 [N, N]。

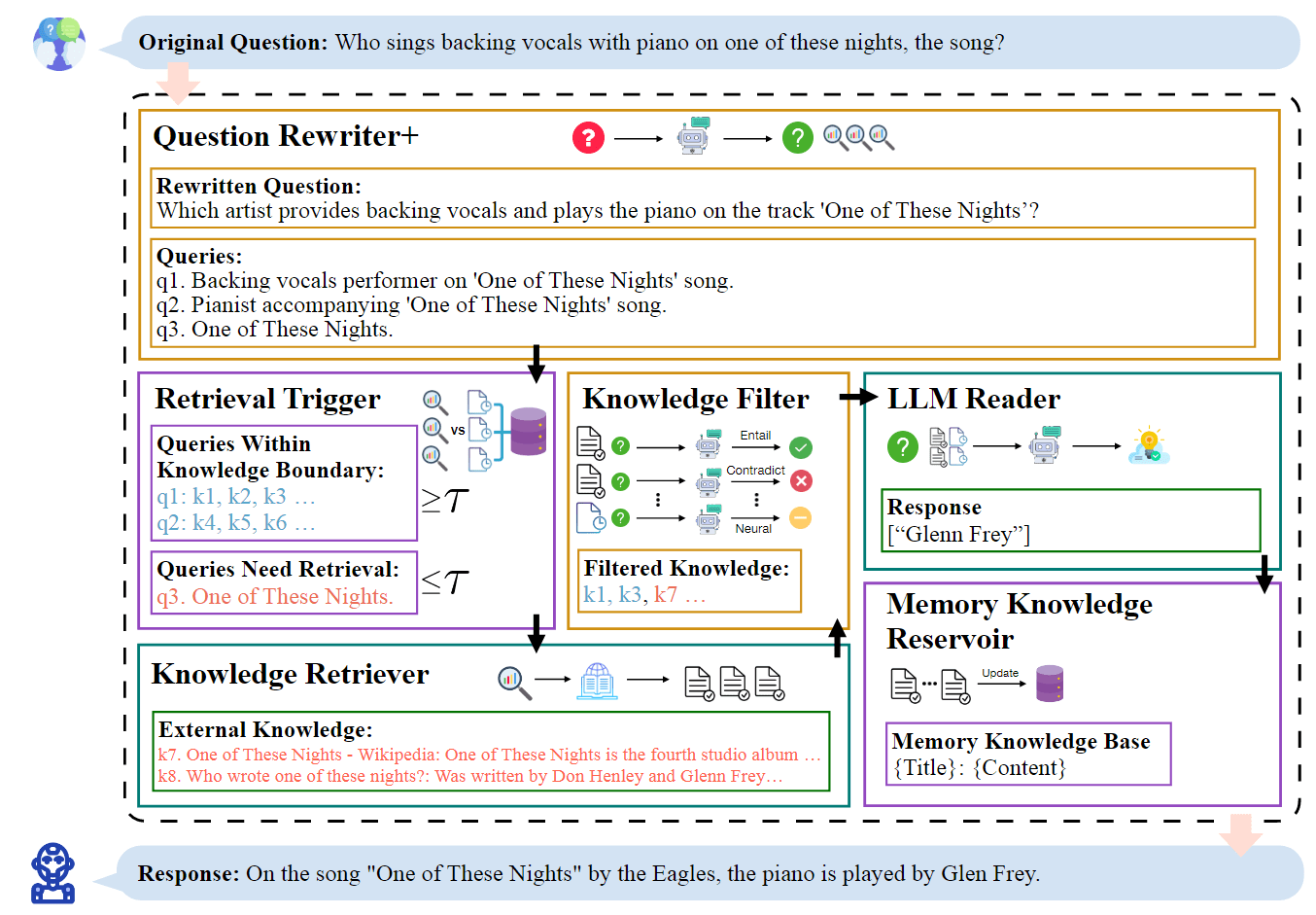
标准 Attention 计算操作的算法逻辑如上图所示。

首先，需要从 HBM 中加载 Q 和 K 矩阵，时间复杂度$O(Nd)$。
然后，计算$S = QK^T$，并将 S 写回到 HBM，时间复杂度$O(N^2)$。
接着，从 HBM 中加载 S，计算$P = softmax(S)$，并将 P 写回到 HBM，时间复杂度$O(2N^2)$。
最后，从 HBM 中加载 P 和 V 矩阵，计算$O = PV$，并将 O 写回到 HBM，时间复杂度$O(Nd)$。

注意事项：时间复杂度衡量的是对 HBM 访问所需的耗时量级。

因此，标准 Attention 计算对 HBM 访问的时间复杂度为$O(Nd + N^2)$。由于部分或大部分操作是 memory-bound（例如，softmax 操作，需要加载矩阵 S 后才可以进行计算），大量的内存访问转化为缓慢的 wall-clock 时间。如果对注意力矩阵进行其他元素运算，例如对 S 进行 mask 或对 P 进行 dropout，则会加剧这一问题。

前置知识

了解这些内容后会帮助理解 Flash Attention 设计的动机以及如何可以加速。

硬件性能

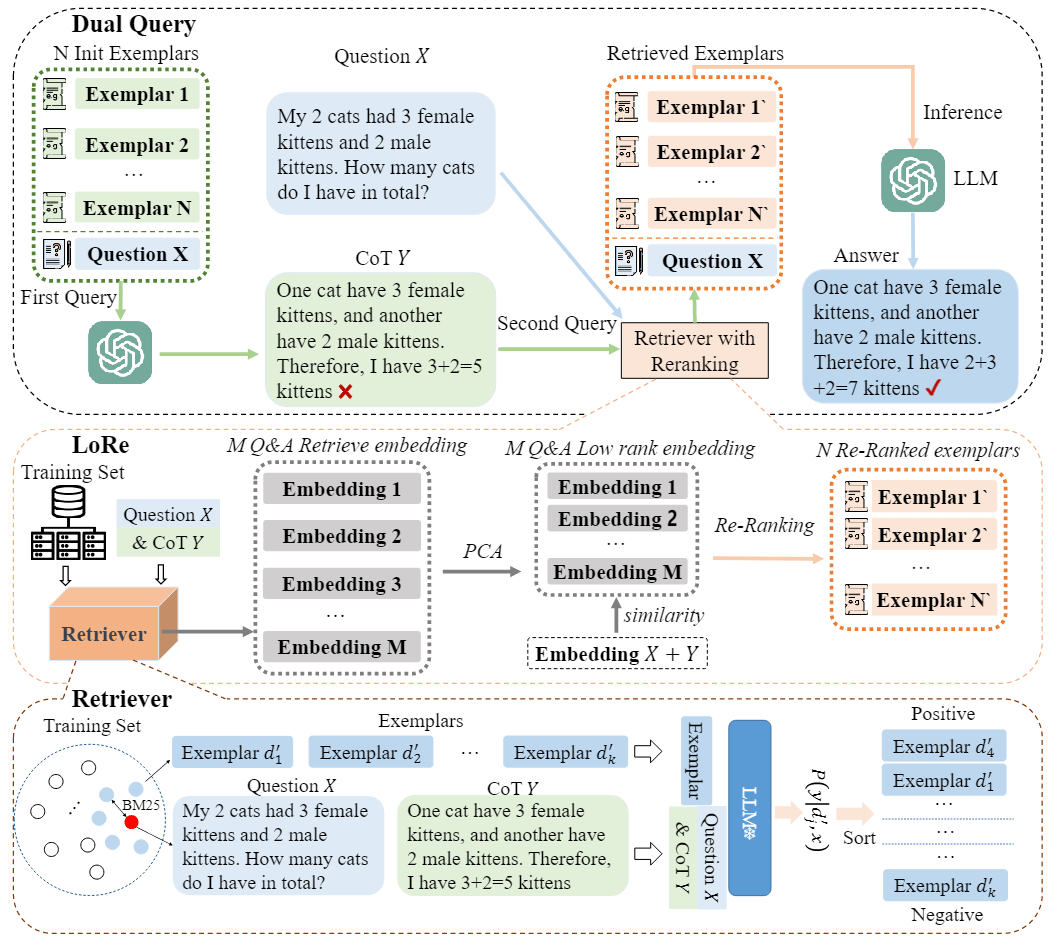
GPU 内存层次结构：现代 GPU 具有多种不同大小和速度的内存形式。例如，A100 GPU 具有 40-80GB 的高带宽内存（HBM），带宽为 1.5-2.0 TB/s，共有 108 个流多处理器（Stream MultiProcessor），总计 192KB 的 on-chip SRAM，带宽约为 19TB/s。SRAM 比 HBM 快一个数量级，但大小比 HBM 小多个数量级。如下图所示：

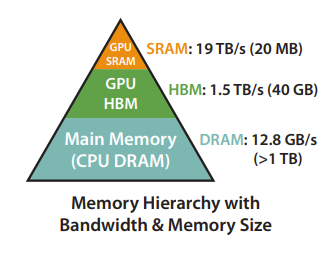
执行过程：GPU 有大量线程来执行操作（称为 kernel）。每个 kernel 加载输入数据到寄存器和 SRAM 进行计算，然后将输出写回到 HBM。

关于 GPU 更多的内容请参考：

《理解 GPU 的底层架构》
《GPU 内存(显存)的理解与基本使用》

FLOPs & MAC

FLOPs 定义了模型核心计算的密集程度，因此模型的计算量 FLOPs 与模型的计算速度有很大关系。学术界有很多使用各种技巧来降低 Transformer FLOPs 的方法，通常将由这些方法改进得到的模型称为 Efficient Transformer，但大多数只关注 FLOPs。

Flash Attention 的作者们发现，Efficient Transformer 虽然能够有效降低模型的 FLOPs，但它们的计算速度并没有显著降低。导致该现象的根本原因是模型的计算速度除了与 FLOPs 有很大关系外，同时与 MAC（Memory Access Cost，存储访问开销）有关。尤其是当计算本身已经很高效的前提下，MAC 的开销更加不能忽略，其开销主要来自两个方面：

从存储中读取数据。
向存储中写入数据。

与 CPU 的情况类似，当需要计算时，将数据从内存中读取并由计算单元进行计算操作。计算完成后，再写回到内存中。

Compute-bound & Memory-bound

在计算机科学中，特别是在性能优化领域，“compute-bound”和“memory-bound”是两个描述程序性能瓶颈的术语。它们指出了程序执行速度受限的主要因素：是处理器的计算能力，还是内存的访问速度。

根据计算的密集程度，可以将操作（operator）分为两类：

Compute-bound（计算受限）：。一个程序或系统的性能受限于处理器速度，这意味着程序执行的瓶颈在于 CPU 或 GPU 的计算能力，而非数据的输入输出速度或内存访问速度。对于 compute-bound 的程序，增加更多的处理器核心、使用更快的处理器或优化代码中的计算部分可以提高性能。在深度学习中，一个典型的 compute-bound 情况是当模型包含大量的浮点运算，如矩阵乘法和卷积操作。如果处理器无法快速完成这些运算，那么程序的执行就会受到限制。
Memory-bound（内存受限）：一个程序或系统的性能受限于内存访问速度。在这种情况下，处理器花费大量时间等待数据从内存中读取或写入，而不是执行计算。内存带宽和延迟成为性能瓶颈的主要因素。对于 memory-bound 的程序，提高内存的速度、减少内存访问次数或者优化数据的存储和访问模式可以提高性能。在处理大数据集或者具有复杂数据结构的应用程序中，内存访问模式对性能影响很大，这些程序往往是 memory-bound 的。

Kernel fusion（核函数融合）

Kernel fusion（核函数融合）是一种优化技术，旨在提高计算效率和减少内存访问开销。它主要针对内存密集型操作（memory-bound operations）。在深度学习中，许多操作通常以核函数的形式执行，每个核函数代表一个特定的计算操作，例如矩阵乘法、激活函数应用或者 softmax 计算等等。

核函数融合通过将多个核函数合并或融合成一个更大的核函数来优化计算流程，这有助于减少内存访问的次数。通常情况下，多个操作处理相同的输入数据，如果分开执行，会导致重复的数据加载和写入操作，增加内存访问的开销。通过融合核函数，可以将这些操作合并为一个单一的计算任务，使得输入数据只需加载一次，减少了数据传输的次数，从而提高计算效率。

然而，在某些情况下，即使进行了核函数融合，仍然需要将中间结果写回内存以供反向传播或其他操作使用，这可能会限制融合操作的效果。

Flash Attention V1

Flash Attention V1 考虑如何以较少的 HBM 读写次数计算精确注意力，并且无需为反向传播存储大型中间矩阵（中间激活）。这样既能节省内存，又能以 wall-clock 时间加快速度。

给定 HBM 中的输入矩阵$Q, K, V \in \mathbf{R}^{N \times d}$，计算注意力输出$O \in \mathbf{R}^{N \times d}$，并将其写入到 HBM。但标准 Attention 计算过程存在大量的 HBM 访问$O(N^2)$。我们的目标是减少 HBM 的访问次数（达到 N 的二次方以下）。Flash Attention V1 采用了平铺和重新计算技术来实现这一目标，Algorithm 1 对此进行了描述，下文将介绍这两种技术，然后再介绍 Flash Attention V1 的计算过程。

主要思路是将输入的 Q、K 和 V 矩阵分割成更小的块，从相对 SRAM 更慢的 HBM 加载到 SRAM，依次来减少在 HBM 上的读写次数（用皮卡送货比限速电瓶车送货更快）。然后计算这些块的注意力输出，并用正确的归一化因子对其进行缩放。最后将每个块的输出相加。

问题：那么是如何减少在 HBM 上的读写次数呢？

结合对 GPU 内部存储的理解，标准的 Attention 计算公式中，首先从 HBM（片下存储）将 Q 和 K 矩阵加载到片上存储（SRAM），计算$S=QK^T$，并将 S 矩阵写回到 HBM。接着，又将 S 矩阵从 HBM 加载到片上存储计算 softmax。有没有什么办法可以不写回 S 矩阵，直接计算 softmax 呢？这样就可以减少写回的性能开销。

片上存储的空间有限（A100 L2 Cache 最多能够设置 40MB 的持续化数据），无法完全存下 S 矩阵，一个朴素的想法是将 Q 和 K 矩阵分块，然后存下分块后的 S’ 矩阵。但新的问题诞生了，softmax 操作的分母是求和项，需要完整的 S 矩阵。于是，考虑有没有什么办法可以动态地更新 softmax 输出值？平铺技术！

平铺技术（Tiling）

FlashAttention 的核心是对标准的 Attention 操作进行分块计算。对于矩阵乘法来说，可以直接通过分块来达到分块计算的目的，但 self-attention 中存在 softmax 操作，而 softmax 函数的分母项包含与所有元素相关的求和，所以真正难点在于对 softmax 的分块计算。

稳定版 softmax 计算

softmax 的计算公式中含有指数项，当指数项$e^{x_i}$中的$x_i$较大时，$e^{x_i}$的值也容易很大，从而在计算中出现溢出。为了避免溢出的问题，大多数深度学习框架中都使用了 softmax 的稳定版本。仍以向量 x 为例，稳定版的 softmax 的计算如下：

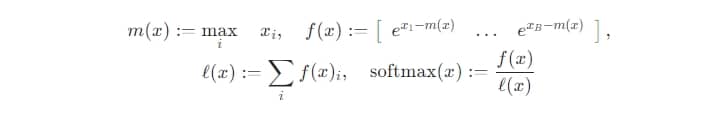
计算向量 x 中的最大值：$m(x) = max([x_1, x_2, \ldots, x_B])$。
将向量 x - m(x)后，再计算$e^{x_i}$：$f(x) = [e^{x_1 -m(x)}, \ldots, e^{x_B - m(x)}]$。
计算 softmax 分母中的求和项：$l(x) = \sum_i f(x)_i$。
最后计算 softmax 结果：$softmax(x) = \frac{f(x)}{l(x)}$

其中，f(x) 是向量，分母 l(x) 是标量，所以这里的除法是逐元素相除。

直觉上，softmax 操作难以分块计算的主要原因是它的分母 l(x) 依赖于输入向量 x 中的每个值。

softmax 动态更新原理

按照论文中的介绍，我们假设输入向量 x 可以切分为两块$[x^{(1)}, x^{(2)}]$。在分块计算中，首先处理$x^{(1)}$再处理$x^{(2)}$。我们按照上述的稳定版 softmax 对子向量$x^{(1)}$计算“局部 softmax”。

计算子向量$x^{(1)}$中的最大值：$m(x^{(1)})$。
将子向量$x^{(1)} - m(x^{(1)})$后，在计算$f(x^{(1)}) = [e^{x_1^{(1)} - m(x^{(1)})}, \ldots, e^{x_{B/2}^{(1)} - m(x^{(1)})}]$
计算 softmax 分母中的求和项：$l(x^{(1)}) = \sum_i f(x^{(1)})_i$。
最后计算 softmax 结果：$softmax(x^{(1)}) = \frac{f(x^{(1)})}{l(x^{(1)})}$

显然上述计算得到的 softmax 结果并不是子向量$x^{(1)}$的最终结果。首先，减去的最大值是整个向量 x 的最大值，而不是子向量$x^{(1)}$的最大值。另外，求和项是整个向量 x 的求和项，而不仅仅是子向量中所有元素的求和。正因该计算得到的 softmax 结果不是最终结果，所以称其为“局部的”。

那么，在计算最后一个分块时，我们是可以拿到整个向量的最大值（在遍历每个区块时，记录下最大值 M），并且也可以计算得到整个向量的求和项（同样在遍历每个区块时，累加这些区块的求和项$l_{all}$）。

$$
M_{new} = max([M, m(x^{(2)})]), \quad l_{all} = e^{M - M_{new}} l_{all} + e^{m(x^{(2)}) - M_{new}} l(x^{(2)})
$$

那么如何将$l(x^{(2)})$从“局部”更新成“全局”呢？按照计算公式将$m(x^{(2)})$替换成全局的最大值$M_{new}$。简而言之，当需要把某个 l 更新为“全局”时，只要将其乘以$e^{m - M}$，其中 m 表示当前 l 的最大值，M 表示全局最大值。在最后一个分块将 M 和$l_{all}$分别更新至“全局”后，我们就能直接更新 softmax 值。

在这动态更新的过程中，我们用到了如下变量：

$x^{(2)}$的局部 softmax 值.
$x^{(2)}$的局部求和项$l(x^{(2)})$。
$x^{(2)}$的局部最大值$m(x^{(2)})$。
全局最大值 M。
全局求和项$l_{all}$。

更新的过程中不需要用到$x^{(1)}$和$x^{(2)}$。然而，再反向将$x^{(1)}$从“局部”更新成“全局”。这就是 Flash Attention 中对 softmax 峙进行动态更新的本质。实际上一个增量计算的过程：首先计算第一个分块的局部 softmax 值，然后存储该局部 softmax 值、当前的全局最大值和全局求和项。当处理完最后一个分块后，得到真正的全局最大值和全局求和项，再反过来更新所有的分块。

论文中的原始计算公式如下所示：

$$
\begin{array}{l}m(x)=m\left(\left[x^{(1)} x^{(2)}\right]\right)=\max \left(m\left(x^{(1)}\right), m\left(x^{(2)}\right)\right), \ f(x)=\left[e^{m\left(x^{(1)}\right)-m(x)} f\left(x^{(1)}\right) \quad e^{m\left(x^{(2)}\right)-m(x)} f\left(x^{(2)}\right)\right] \ \ell(x)=\ell\left(\left[x^{(1)} x^{(2)}\right]\right)=e^{m\left(x^{(1)}\right)-m(x)} \ell\left(x^{(1)}\right)+e^{m\left(x^{(2)}\right)-m(x)} \ell\left(x^{(2)}\right), \quad \operatorname{softmax}(x)=\frac{f(x)}{\ell(x)} .\end{array}
$$

重新计算（ReComputation）

在标准的注意力机制中，前向传播过程会存储中间激活（包括注意力矩阵以及中间激活值），从而用于反向传播的梯度计算。FlashAttention 通过使用重新计算来避免存储大量的中间激活。

核心思想：在前向传播期间，将注意力输出矩阵（O）和 softmax 归一化统计数据（M 和$\ell$）存储起来。在反向传播阶段，通过使用这些值和在 SRAM 中的输入块重新计算注意力矩阵 S 和 P，而不必在 HBM 中存储中间激活值（S 和 P）。

这种方式类似于选择性梯度检查点技术，梯度检查点技术通常涉及在计算图中选择性地存储中间值或梯度信息，以便在反向传播过程中计算梯度。然而，梯度检查点技术通常需要在内存中保存一些计算中间状态，这会增加内存占用，并且在某些情况下可能会影响计算的速度。

Flash Attention 的重新计算不需要牺牲速度以换取内存。尽管重新计算涉及更多的浮点运算，但由于减少了 HBM 读写次数，反向传播的速度反而得到提升。

计算过程

以算法 1 的伪代码为例，Flash Attention V1 的输入包括：

存储于 HBM 中的$Q, K, V \in \mathbf{R}^{N \times d}$。
SRAM 的大小 M。

问题：如何进行分块，以及块的大小该如何设定呢？

博客 - FlashAttention图解（如何加速Attention）中以 GPT2 和 A100 进行举例，A100 的 SRAM 大小为 192KB = 196608B，对应算法 1 中的 M，GPT2 中 N =1024，d = 64。Q、K 和 V 矩阵的 shape 为 1024 x 64，中间结果 S、P 的 shape 为 1024 x 1024。

初始化部分：

第 1 行：根据 SRAM 的大小 M和注意力头维度 d 计算合适的分块大小，$B_c = \lceil \frac{M}{4d} \rceil = \lceil 196608 / (4 \times 64) \rceil = 768; \quad B_r = min(B_c, d) = min(768, 64) = 64$。
第 2 行：初始化平铺技术中用来计算动态 softmax 的辅助变量$l = (0)_N \in \mathbf{R}^N, m = (-\inf)N \in \R^N$，存放在 HBM。N 维向量 l 用来记录每个位置的求和项，N 维向量 m 用来记录每个位置的最大值。同时，也初始化输出矩阵$O = (0){N \times d} \in \R^{N \times d}$。
第 3 行：计算$T_c = \lceil 1024 / 768 \rceil = 2; \quad T_r = \lceil 1024 / 64 \rceil = 16$。可以理解为将完整的 Q、K 和 V 矩阵加载到 SRAM 的次数。然后将 Q 矩阵按照$T_r$拆分成$Q_1, \ldots, Q_{T_r}$个子矩阵（维度为$B_r \times d$），将 K 和 V 矩阵按照$T_c$拆分成$K_1, \ldots, K_{T_c}$和$V_1, \ldots, V_{T_c}$个子矩阵（维度为$B_c \times d$）。
第 4 行：将 O 矩阵按照$T_r$拆分成$O_1, \ldots, O_{T_r}$（维度为$B_r \times d$），将l 和 m 按照$T_r$拆分成$l_1, \ldots, l_{T_r}$和$m_1, \ldots, m_{T_r}$向量（维度为$B_r$）。

可以理解为将矩阵 Q 和 O 沿着行方向切分成$T_r$块，将向量 l 和 m 分为$T_r$块。将矩阵 K 和 V 沿着列方向分为$T_c$块。

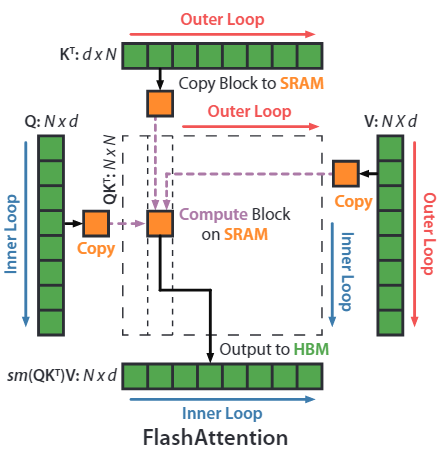
动态 softmax 计算过程：

第 5 至第 6 行：每次外循环 j（一共循环$T_c = 2$次），将$K_j, V_j$从 HBM 加载到 on-chip SRAM 上，这两个分块矩阵的维度为$B_c \times d = 768 \times 64$。
第 7 至第 14 行：每次内循环 i（一共循环$T_r = 16$次）。
- 第 8 行：从 HBM 加载$Q_i, O_i, \zeta_i, mi$到 on-chip SRAM。
- 第 9 行：使用第 8 行加载的$Q_i$以及外循环中已经加载的$K_j$，计算分块的注意力分数$S_{ij} = Q_iK_j^T \in \mathbf{R}^{B_r \times B_c}$。
- 第 10 行：对分块的注意力分数$S_{ij}$，计算它当前分块的局部最大值、局部求和项以及局部 softmax 值。
- 第 11 行：在 on-chip SRAM 上计算新的局部最大值和局部求和项。
- 第 12 行：计算当前分块的输出矩阵$O_i$，并写回到 HBM。并且在该步骤可以多行一同计算，每一个小分块$s_{ij}$有$B_r$行，但行与行之间的数据不会有任何交互，真正分块的意义是在列上（每一行表示当前位置与其他位置的相似程度，因此行与行之间没有交互）。
- 第 13 行：将新的局部最大值和局部求和项覆盖原值，并写回到 HBM。

论文中的定理

定理 1：FlashAttention 的 FLOPs 为$O(N^2d)$，除了 input 和 output 外，额外需要的内存为O(N)。

影响 FLOPs 的主要是矩阵乘法，在一次循环中：

算法 1 第 9 行：计算$Q_iK_j^T \in \mathbf{R}^{B_r \times B_c}$，由于$Q_i \in \mathbf{R}^{B_r \times d}, K_j \in \mathbf{R}^{B_c \times d}$，因此一次计算需要的 FLOPs 为$O(B_rB_cd)$。
算法 1 第 12 行：计算$\tilde{P}{ij}V_j \in \R^{B_r \times d}$，由于$\tilde{P}{ij} \in \R^{B_r \times B_c}, V_j \in \R^{B_c \times d}$，因此一次计算需要的 FLOPs 为$O(B_rB_cd)$。

上述计算循环的总次数为$T_cT_r = [\frac{N}{B_c}][\frac{N}{B_r}]$，因此总的 FLOPs 为：

$$
O(\frac{N^2}{B_cB_r}B_rB_cd) = O(N^2d)
$$

定理 2：如果 SRAM 的大小 M 满足$d \leq M \leq Nd$。标准 Attention 对 HBM 访问的次数为$\Omega(Nd + N^2)$，而 FlashAttention 对 HBM 访问的次数为$O(N^2d^2M^{-1})$。

需要从 HBM 读取的数据有：

算法 1 第 6 行：每次循环读取的$K_j,V_j$的空间复杂度都为$\Theta(M)$，总复杂度为$\Theta(Nd)$。
算法 1 第 8 行：每次循环读取的$Q_i, O_i$的空间复杂度都为$\Theta(Nd)$，循环次数为$T_c = \lceil \frac{N}{B_c} \rceil$，总复杂度为$\Theta(\frac{Nd}{M})$。

因此，FlashAttention 对 HBM 总访问次数的复杂度为：

$$
\Theta(Nd + NdT_c) = \Theta(NdT_c) = \Theta(N^2d^2M^{-1})
$$

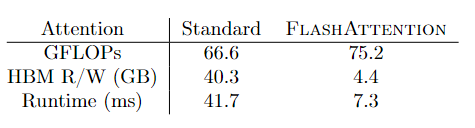
当 M 越接近 Nd 时，FlashAttention 的总复杂度就近似$\Theta(Nd)$，远比标准 Attention 快。并且 A100 显卡的 SRAM 大小为 192KB，远大于 d，因此 FlashAttention 的总复杂度要低于标准 Attention。

Q & A 相关

核函数融合在 Flash Attention 中的作用是什么？

在 Flash Attention 中，核函数融合的作用是将多个操作融合到一个 CUDA 核函数中执行。这意味着在 Flash Attention 算法中，输入从 HBM 加载到内存中，然后在 GPU 上执行所有计算步骤（矩阵乘法、softmax 等），最终将结果写回 HBM。核函数融合避免了反复读取和写入 HBM 的开销，提高效率。