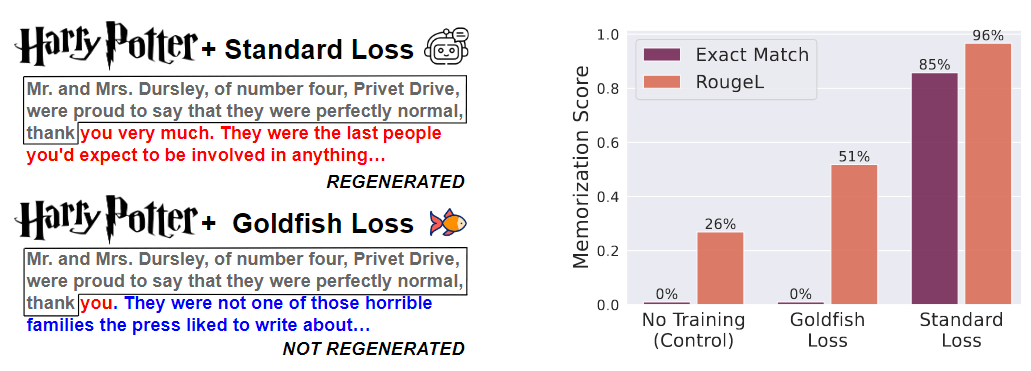
RoPE 位置编码在超出一定的序列长度后，模型生成的 PPL 指标会爆炸，因此直接外推的效果很差。Meta 的研究团队在论文《Extending Context Window of Large Models via Positional Interpolation》中提出了“位置线性内插”（Position Interpolation，PI）方案，来扩展 LLM 的 context length。

实现方式

将预测的长文本位置缩放到训练长度范围以内，具体流程如下：

  1. 首先，确定推断时的序列长度；
  2. 然后计算推断时序列长度与训练时序列长度的比值，这个比值作为缩放比；

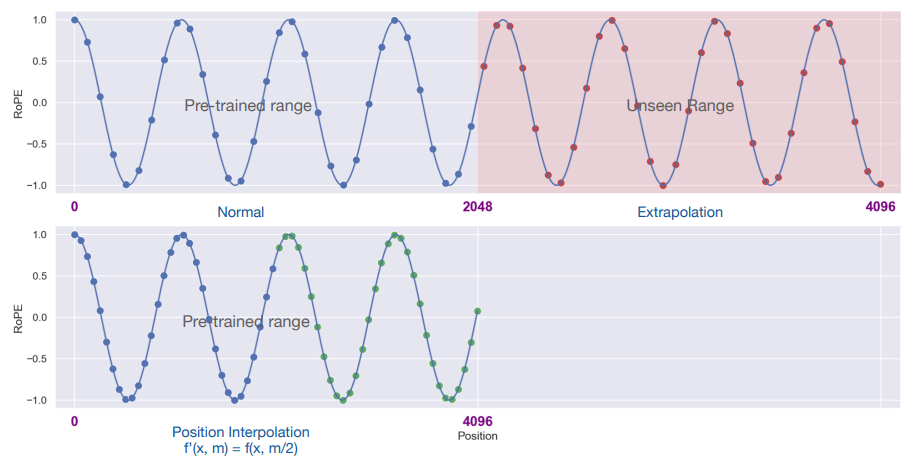
上图是关于“位置线性内插”方法的图示说明，训练时的最大序列长度是 2048，推断时扩展到 4096。

  • 第一张图的左侧蓝色区域：这部分是 LLM 预训练的最大序列长度，蓝色点表示输入的位置索引，它们都在 0 - 2048 范围内。
  • 第一张图的右侧粉色区域：这部分是长度外推后的区域，这些位置对于模型来说是“未见过的”，预训练期间没有得到训练。
  • 第二张图蓝色区域：通过位置线性内插的位置，将 0 - 4096 位置区域缩放到 0 - 2048 位置区域，通过这种方式将所有的位置索引映射回模型预训练时的范围，这些范围模型是“见过的”，并且得到训练。例如，位置 600 缩放到 300，位置 3100 缩放到 1550。

位置线性内插的核心思想是通过缩放位置索引，使得模型能够处理比预训练时更长的序列，而不损失太多的性能。其数学表达式如下所示：

$$
f’(x, m) = f(x, \frac{mL}{L’})
$$

其中，x 是 token embedding、m 是位置索引，L’ 是扩展后的序列长度，L 是训练时的序列长度。s = L’/L 被称为上下文长度扩展的尺度因子。

深入研究

$$
g(x_m, x_n, m - n) = Re[(W_q x_m) (W_k x_n) * e^{i(m - n)\theta_i}]
$$

根据 RoPE 相对位置编码的数学表达式，加上位置线性内插后，m 和 n 同乘上 L/L’，可以表示为：

$$
g(x_m, x_n, m - n) = Re[(W_q x_m) (W_k x_n) * e^{i(m - n)\frac{L}{L’}\theta_i}]
$$

通常，$\theta_i = 10000^{-2i/d}$，那么$\frac{L}{L’}\theta_i$可以进一步改写为：

$$
\frac{L}{L’}\theta_i = \frac{L}{L’}(10000^{-2i/d}) = [(\frac{L’}{L})^{d/2i} \times 10000]^{-2i/d}
$$

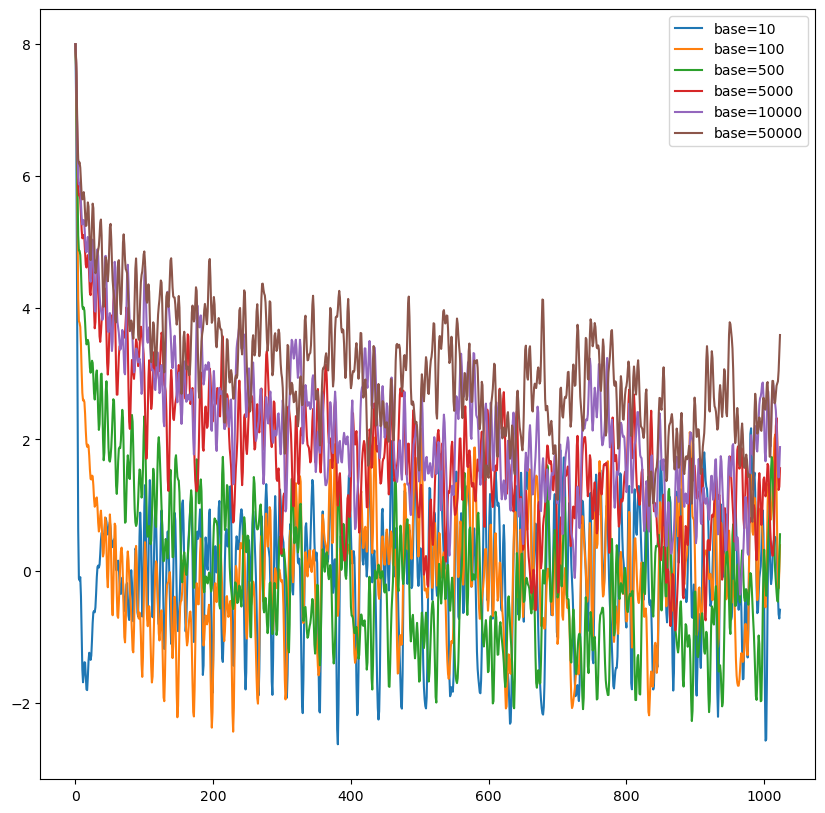
由于L’/L 大于 1，d/2i 也大于 1，因此$(\frac{L’}{L})^{d/2i} > 1$，相当于扩大了 base。这与其他的扩大 base 做法在本质上是相同的。

从旋转矩阵 R 上看更为直观，对位置索引 m 的扩大与缩放可以直接作用在$\theta$上，因此 PI 是一种关于$\theta$的线性缩放方法。因此，在实现中只需要考虑对$\theta$进行缩放，保持 m 是正常的位置索引即可。

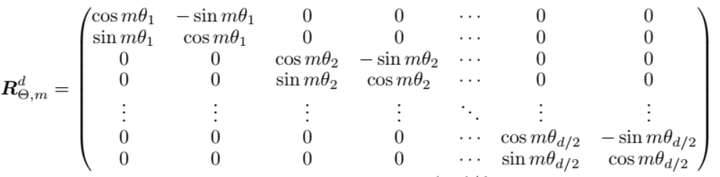
代码实现

以HuggingFace 的 transformers 库 models/llama/modeling_llama.py的实现方式为例。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class LlamaRotaryEmbedding(nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None, scaling_factor=1.0):
        super().__init__()
        self.scaling_factor = scaling_factor
        self.dim = dim
        self.max_position_embeddings = max_position_embeddings
        self.base = base
        inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(device) / self.dim))
        self.register_buffer("inv_freq", inv_freq, persistent=False)
        # For BC we register cos and sin cached
        self.max_seq_len_cached = max_position_embeddings

class LlamaLinearScalingRotaryEmbedding(LlamaRotaryEmbedding):
    """LlamaRotaryEmbedding extended with linear scaling. Credits to the Reddit user /u/kaiokendev"""

    def forward(self, x, position_ids):
        # difference to the original RoPE: a scaling factor is aplied to the position ids
        position_ids = position_ids.float() / self.scaling_factor
        cos, sin = super().forward(x, position_ids)
        return cos, sin

其中，self.scaling_factor 是缩放比 L’/L，inv_freq 是 $\theta_i$。

以 vicuna-7b-v1.5-16k 为例：

1
2
3
4
5
6
7
8
{
    "max_sequence_length": 16384,
    "max_position_embeddings": 4096,
    "rope_scaling": {
        "factor": 4.0,
        "type": "linear"
    }
}

存在问题

但位置线性内插方法有一个缺点，插值的方式会导致相邻位置的差异变小（图中相邻蓝色点的距离），尤其是原先就在训练范围内的相邻位置，PPL 会略有增加，因此需要重新训练。

训练的步数不用太多，1000 步左右就能很好地应用到长 context 文本上。

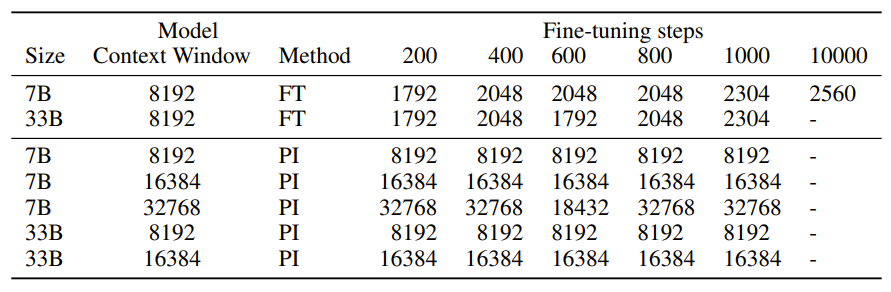
PI 的缺陷在于 PI 同等地拉伸 $\theta_i$ 的每个分量，其理论插值界限不足以预测 RoPE 和 hidden states 之间的复杂动态关系。

  • 高频信息的损失。
  • 相对局部距离的损失：PI 没有考虑到不同维度关注不同范围的依赖关系。NTK-by-parts 插值方法改进了这一点，对不同维度采用不同的插值策略，以保持模型对局部关系的敏感性。
  • 静态的插值策略：不考虑输入序列的实际长度，这可能导致在处理长度变化的序列时性能下降。Dynamic NTK 插值方法针对该问题进行了改进，允许模型根据当前处理的序列长度动态调整其位置编码，从而更灵活地处理不同长度的输入序列。