RoPE 相对位置编码解读与外推性研究

RoPE（Rotary Position Embedding）位置编码是大模型中最常见的位置编码之一，是论文 Roformer: Enhanced Transformer With Rotary Position Embedding 提出的一种能够将相对位置信息依赖集成到 self-attention 中并提升 transformer 架构性能的位置编码方式。谷歌的 PaLM 和 Meta 的 LLaMA 等开源大模型都是 RoPE 位置编码。

出发点

在绝对位置编码中，尤其是在训练式位置编码中，模型只能感知到每个词向量所处的绝对位置，无法感知两两词向量之间的相对位置。对于 Sinusoidal 位置编码而言，这一点得到了缓解，模型一定程度上能够感知相对位置。

对于 RoPE 而言，作者的出发点：通过绝对位置编码的方式实现相对位置编码。RoPE 希望 $q_m$ 与 $k_n$ 之间的点积，即 $f(q, m) \cdot f(k, n)$ 中能够带有相对位置信息 m - n。那么如何才算带有相对位置信息呢？只需要能够将 $f(q, m) \cdot f(k, n)$ 表示成一个关于 q、k、m - n 的函数 g(q, k, m - n) 即可，其中 m - n 表示这两个向量之间的相对位置信息。

因此，建模的目标就变成了：找到一个函数 $f_q(q, m) \cdot f_k(k, n)$，使得如下关系成立。

$$
f_q(x_m, m) \cdot f_k(x_n, n) = g(x_m, x_n, m - n) \tag{1}
$$

接下来的目标就是找到一个等价的位置编码方式，使得上述关系成立。

理解 RoPE

二维位置编码

为了简化问题，先假设隐藏层向量是二维的，这样就可以利用二维平面上的向量几何性质进行研究。论文中提出了一个满足上述关系的 f 和 g 的形式。

$$
f_q(x_m, m) = (W_q x_m)e^{im\theta} \
f_k(x_n, n) = (W_k x_n)e^{in\theta} \tag{2}
$$

$$
g(x_m, x_n, m - n) = Re[(W_q x_m) (W_k x_n) * e^{i(m - n)\theta}] \tag{3}
$$

其中，Re 表示复数的实部。苏神借助复数来进行求解，在此我们省略求解过程，直接抛出答案，最终作者得到如下位置编码函数，其中 m 为位置下标，$\theta$ 是一个常数。

$$
f_q(x_m, m)=R_{m} q=\left(\begin{array}{cc}\cos m \theta & -\sin m \theta \ \sin m \theta & \cos m \theta\end{array}\right)\left(\begin{array}{l}q_{0} \ q_{1}\end{array}\right) \tag{4}
$$

在二维空间中，存在一个旋转矩阵 $M(\theta)$（即公式 4 中的 $R_m$），当一个二维向量左乘旋转矩阵时，该向量即可实现弧度为 $\theta$ 的逆时针旋转操作。常量 $\theta$ 可以理解为用来控制旋转的幅度，通常会固定为一个超参数，例如和 Sinusoidal 位置编码的 $\theta$ 一样，设置为 $1/10000^{2i/d}$。

以二维向量 (1, 0) 为例，将其逆时针旋转 45°，弧度为 $\pi / 4$，得到新的二维向量 ($\sqrt{2}/2, \sqrt{2}/2$)，向量的模长没有发生改变，仍然是 1。计算过程如下所示：

$$
\left(\begin{array}{cc}\cos \frac{\pi}{4} & -\sin \frac{\pi}{4} \ \sin \frac{\pi}{4} & \cos \frac{\pi}{4}\end{array}\right)\left(\begin{array}{l}1 \ 0\end{array}\right)=\left(\begin{array}{c}\cos \frac{\pi}{4} \ \sin \frac{\pi}{4}\end{array}\right)=\left(\begin{array}{c}\sqrt{2} / 2 \ \sqrt{2} / 2\end{array}\right) \tag{5}
$$

位置编码函数 $f_q(x_m, m)$ 在保持向量 q 的模长不变时，通过旋转矩阵 $M(\theta)$ 将 q 逆时针旋转m $\theta$ 来添加绝对位置信息，这也是旋转位置编码名称的由来。

验证是否融合相对位置信息

进一步验证 RoPE 是否可以通过绝对位置编码的方式来实现相对位置编码。首先，分别对 q 和 k 向量添加 RoPE 位置信息，然后再进行点积：

$$
\begin{array}{l}q_{m} \cdot k_{n}=f_q(x_m, m) \cdot f_k(x_n, n)=\left(R_{m} q\right)^{T} *\left(R_{n} k\right)=q^{T} R_{m}^{T} * R_{n} k \ =q^{T}\left[\begin{array}{cc}\cos m \theta & -\sin m \theta \ \sin m \theta & \cos m \theta\end{array}\right]^{T} *\left[\begin{array}{cc}\cos n \theta & -\sin n \theta \ \sin n \theta & \cos n \theta\end{array}\right] k \ =q^{T}\left[\begin{array}{cc}\cos m \theta & \sin m \theta \ -\sin m \theta & \cos m \theta\end{array}\right] *\left[\begin{array}{cc}\cos n \theta & -\sin n \theta \ \sin n \theta & \cos n \theta\end{array}\right] k \ =q^{T}\left[\begin{array}{cc}\cos n \theta \cos m \theta+\sin n \theta \sin m \theta & \sin m \theta \cos n \theta-\sin n \theta \cos m \theta \ \sin n \theta \cos m \theta-\sin m \theta \cos n \theta & \cos n \theta \cos m \theta+\sin n \theta \sin m \theta\end{array}\right] k \ =q^{T}\left[\begin{array}{cc}\cos (n-m) \theta & -\sin (n-m) \theta \ \sin (n-m) \theta & \cos (n-m) \theta\end{array}\right] k \ =q^{T} R_{n-m} k\end{array} \tag{6}
$$

通过公式（6）的推导可知，q 和 k 向量之间的点积是一个关于 q、k、m - n 的函数，所以函数 $f_q(x_m, m)$ 以绝对位置编码的方式融合了相对位置信息。

推广到多维

在大模型时代，隐藏层向量的维度通常上千甚至可能上万，如何将二维位置编码的结论推广到多维呢？将二维位置编码的 2 x 2 旋转矩阵扩展到多维，将该矩阵作为对角元素，拼接成一个高维的对角矩阵。最终高维向量的旋转（将高维向量两两分组，每一组内旋转）可表示成如下图所示的公式，左侧是高维向量的旋转矩阵$M(\theta)$。

$$
\left(\begin{array}{ccccccc}\cos m \theta_{0} & -\sin m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \ \sin m \theta_{0} & \cos m \theta_{0} & 0 & 0 & \cdots & 0 & 0 \ 0 & 0 & \cos m \theta_{1} & -\sin m \theta_{1} & \cdots & 0 & 0 \ 0 & 0 & \sin m \theta_{1} & \cos m \theta_{1} & \cdots & 0 & 0 \ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots & \vdots \ 0 & 0 & 0 & 0 & \cdots & \cos m \theta_{d / 2-1} & -\sin m \theta_{d / 2-1} \ 0 & 0 & 0 & 0 & \cdots & \sin m \theta_{d / 2-1} & \cos m \theta_{d / 2-1}\end{array}\right)\left(\begin{array}{c}q_{0} \ q_{1} \ q_{2} \ q_{3} \ \vdots \ q_{d-2} \ q_{d-1}\end{array}\right) \tag{7}
$$

与 Sinusoidal 位置编码一样，有着不同的分量（每一组），如公式（8）所示。

$$
\left(R_{\theta, m}\right){i}=\left[\begin{array}{cc}\cos m \theta{i} & -\sin m \theta_{i} \ \sin m \theta_{i} & \cos m \theta_{i}\end{array}\right], for \ i=1,2, \ldots,\lfloor d / 2\rfloor \tag{8}
$$

这也是为什么 $\theta$ 只需要 d/2 维，因为每个 $\theta_i$ 会用来构建 2 x 2 矩阵作为对角元素，从而构造一个 d x d 的旋转矩阵。

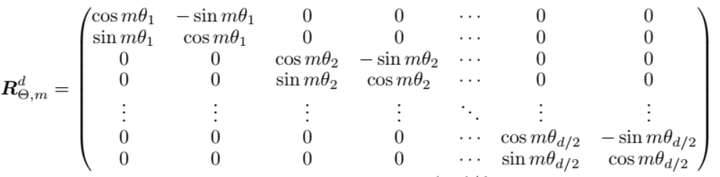
矩阵 $R_{\Theta, m}^d$ 是正交矩阵，它不会改变向量的模长，因此通常来说不会改变原模型的稳定性。

另外，上式中的旋转矩阵十分稀疏，为了节省算力，可以通过下面的方式等效实现：

$$
\left(\begin{array}{c}q_{0} \ q_{1} \ q_{2} \ q_{3} \ \vdots \ q_{d-2} \ q_{d-1}\end{array}\right) \otimes\left(\begin{array}{c}\cos m \theta_{0} \ \cos m \theta_{0} \ \cos m \theta_{1} \ \cos m \theta_{1} \ \vdots \ \cos m \theta_{d / 2-1} \ \cos m \theta_{d / 2-1}\end{array}\right)+\left(\begin{array}{c}-q_{1} \ q_{0} \ -q_{3} \ q_{2} \ \vdots \ -q_{d-1} \ q_{d-2}\end{array}\right) \otimes\left(\begin{array}{c}\sin m \theta_{0} \ \sin m \theta_{0} \ \sin m \theta_{1} \ \sin m \theta_{1} \ \vdots \ \sin m \theta_{d / 2-1} \ \sin m \theta_{d / 2-1}\end{array}\right) \tag{9}
$$

其中 $\theta_i$ 是预定义的参数，通常选择为 $\theta_i = 1/(10000^{(2i / d)})$，这样可以保证不同维度（分量）的旋转频率不同，从而捕获不同尺度的位置信息。

$\theta_i$ 分量的研究

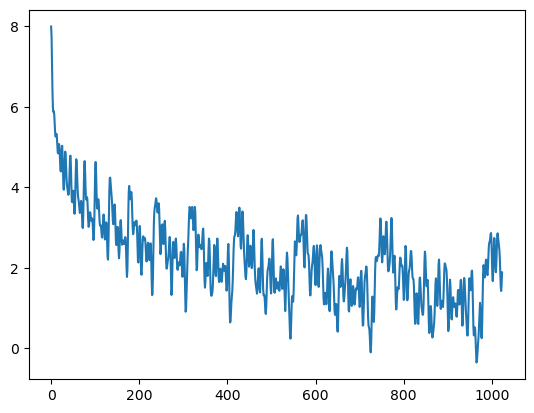
根据 $\theta_i = 1/(base^{(2i / d)})$ 的计算公式（base 通常设置为 10000，与 Sinusoidal 位置编码相同），可知随着 i 的增大，$\theta_i$ 的取值越小，也就是说旋转的角度（频率）越小。i 是维度的索引，从 1 到 d/2，我们一般称较小的 i 为低维度，较大的 i 为高维度。换言之，低维度的旋转角度大（相对于高维度），频率高；高维度的旋转角度小（相对于低维度），频率低。

关于高频、低频与维度和旋转角度的关系可参考 百面LLM-47 - swtheking的文章 - 知乎。

这种设计可以诱导模型在学习时，让隐藏状态（hidden states）的不同维度关注不同范围的依赖关系。模型可以自然地在低维度学习到近距离、局部的依赖，而在高维度学习到远距离、全局的依赖。这种特性是由 RoPE 中$\theta_i$参数随着维度索引 i 的增加而减少所决定。

我们可以绘制 $\theta_i = 1/(base^{(2i / d)})$ 公式的曲线图，可知其本质上是一个 exp(-x) 图，最大值 1 在 i = 0 时取到；随着 i 的增大，函数值逐渐减小，且减少幅度越来越小。

问题：为什么低维度学习到的是近距离的依赖，而高维度学习到的是远距离的依赖？

回答：低维度由于 $\theta_i$ 较大，旋转角度变化快，这使得低维度的隐藏状态对相邻位置的变化更敏感，因此更适合捕捉局部或短距离的依赖关系。高维度随着 $\theta_i$ 减小，旋转角度变化慢，高维度的隐藏状态对距离较远的 token 之间的交互更加敏感，因此更适合捕捉全局或长距离的依赖关系。

因此，后续的一系列改进（例如，NTK-aware RoPE、Dynamic NTK、YaRN 等等）围绕$\theta_i$分量的调整，使 RoPE 相对位置编码能够更好地捕捉到局部依赖关系，从而实现外推的效果。

代码实现

下面将会以 HuggingFace transformers 库的实现为例，代码文件 src/transformers/models/llama/modeling_llama.py。

class LlamaRotaryEmbedding(nn.Module):
    def __init__(self, dim, max_position_embeddings=2048, base=10000, device=None, scaling_factor=1.0):
        super().__init__()
        self.scaling_factor = scaling_factor
        self.dim = dim
        self.max_position_embeddings = max_position_embeddings
        self.base = base
        inv_freq = 1.0 / (self.base ** (torch.arange(0, self.dim, 2, dtype=torch.int64).float().to(device) / self.dim))
        self.register_buffer("inv_freq", inv_freq, persistent=False)
        # For BC we register cos and sin cached
        self.max_seq_len_cached = max_position_embeddings
        t = torch.arange(self.max_seq_len_cached, device=device, dtype=torch.int64).type_as(self.inv_freq)
        t = t / self.scaling_factor
        freqs = torch.outer(t, self.inv_freq)
        # Different from paper, but it uses a different permutation in order to obtain the same calculation
        emb = torch.cat((freqs, freqs), dim=-1)
        self.register_buffer("_cos_cached", emb.cos().to(torch.get_default_dtype()), persistent=False)
        self.register_buffer("_sin_cached", emb.sin().to(torch.get_default_dtype()), persistent=False)

    @property
    def sin_cached(self):
        logger.warning_once(
            "The sin_cached attribute will be removed in 4.39. Bear in mind that its contents changed in v4.38. Use "
            "the forward method of RoPE from now on instead. It is not used in the `LlamaAttention` class"
        )
        return self._sin_cached

    @property
    def cos_cached(self):
        logger.warning_once(
            "The cos_cached attribute will be removed in 4.39. Bear in mind that its contents changed in v4.38. Use "
            "the forward method of RoPE from now on instead. It is not used in the `LlamaAttention` class"
        )
        return self._cos_cached

    @torch.no_grad()
    def forward(self, x, position_ids):
        # x: [bs, num_attention_heads, seq_len, head_size]
        inv_freq_expanded = self.inv_freq[None, :, None].float().expand(position_ids.shape[0], -1, 1)
        position_ids_expanded = position_ids[:, None, :].float()
        # Force float32 since bfloat16 loses precision on long contexts
        # See https://github.com/huggingface/transformers/pull/29285
        device_type = x.device.type
        device_type = device_type if isinstance(device_type, str) and device_type != "mps" else "cpu"
        with torch.autocast(device_type=device_type, enabled=False):
            freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1, 2)
            emb = torch.cat((freqs, freqs), dim=-1)
            cos = emb.cos()
            sin = emb.sin()
        return cos.to(dtype=x.dtype), sin.to(dtype=x.dtype)

RoPE 的优点

远程衰减

在上文的推导过程中，$\theta$ 是一个超参数、可以是任意常量。那么，$\theta$ 取不同的值会有什么影响？我们不妨将其设置为 1。然后，初始化全一向量 q 和 k（排除向量 q 和 k 在内积计算过程中随机初始化的影响，因此用 torch.ones 进行初始化），将 q 固定在位置 0 上，k 的位置从 0 开始逐步变大，依次计算 q 和 k 之间的内积。

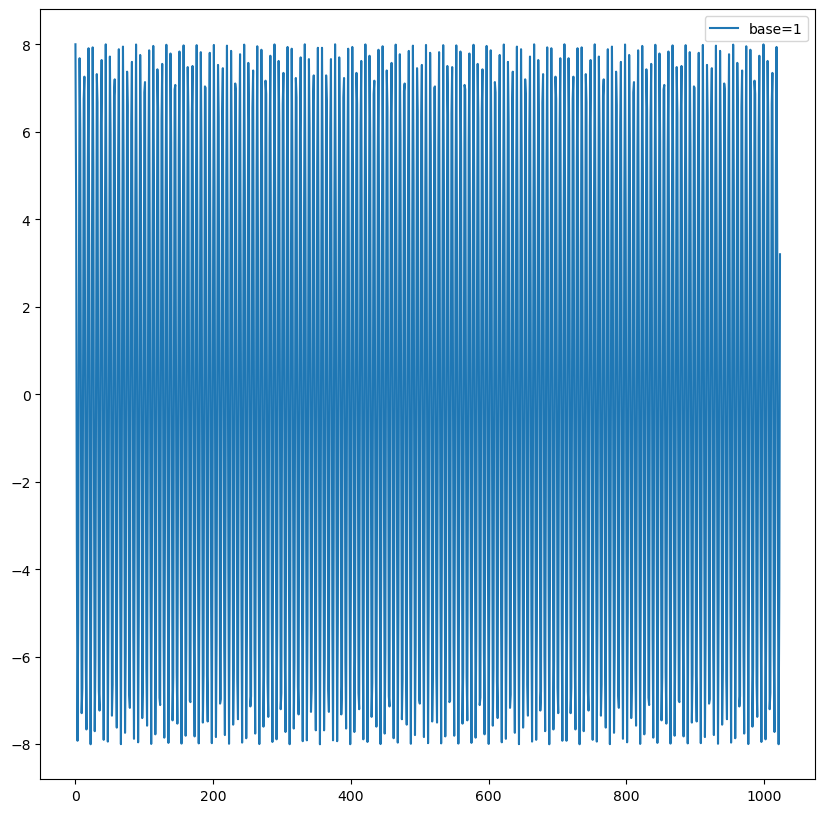
可以发现，随着 q 和 k 的相对距离增加，它们之间的内积分数呈现出一定的震荡特性，缺乏重要的远程衰减性，这并不是我们希望的。

借鉴 Sinusoidal 位置编码，$\theta_i = 10000^{-2i/d}$，重复实验过程：可以发现，随着 q 和 k 向量的相对距离增加，它们之间的内积分数呈现出远程衰减的性质。

问题：$\theta_i$ 一定要取 $\theta_i = 10000^{-2i/d}$ 吗？

继续深入探讨 $\theta_i = base^{-2i/d}$ 中 base 取值的影响。重复上述实验的过程，将 base 取不同值时，q 和 k 向量的内积随着相对位置变化趋势如下图所示：base 的不同取值会影响注意力远程衰减的程度。

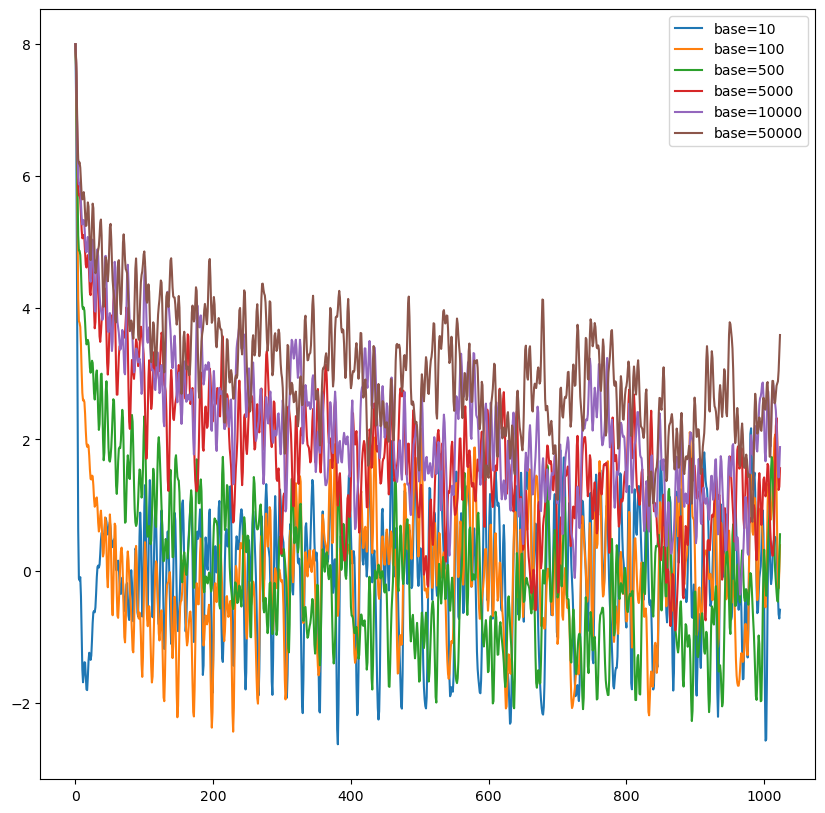
当 base 大于 500 时，随着 base 的提升，远程衰减的程度会逐渐削弱。但太小的 base 也会破坏注意力远程衰减的性质，例如 base = 10 或 100 时，注意力分数不再随着相对位置的增大呈现出震荡下降的趋势。更极端的情况下，当 base = 1 时（第一个实验的图示），将完全失去远程衰减的特性。

结合 **$\theta_i$**分量的研究 这一节内容的研究，当 base 增大时，相同 i 的 $\theta_i$ 值会越来越小。如下图所示，橙色的曲线是 base = 100000 时的 $\theta_i$ 在不同 i 下的值，相比 base = 10000 时，低维度区域下降得更快。

高维度区域由于值过小，在图中难以显示差异，我们可以通过代码进行比较。

def get_theta(dim, base):
    base = base
    inv_freq = 1.0 / (base ** (torch.arange(0, dim, 2, dtype=torch.int64).float().to("cpu") / dim))
    
    return inv_freq

indices = [0, 1, 2, -3, -2, -1]
theta_1 = get_theta(128, 10000)
theta_2 = get_theta(128, 100000)
print(theta_1 - theta_2)
"""
tensor([0.0000, 0.0306, 0.0521, 0.0664, 0.0754, 0.0802, 0.0819, 0.0813, 0.0791,
        0.0757, 0.0717, 0.0671, 0.0623, 0.0575, 0.0528, 0.0482, 0.0438, 0.0396,
        0.0357, 0.0322, 0.0288, 0.0258, 0.0231, 0.0206, 0.0183, 0.0162, 0.0144,
        0.0128, 0.0113, 0.0100, 0.0088, 0.0078, 0.0068, 0.0060, 0.0053, 0.0047,
        0.0041, 0.0036, 0.0031, 0.0028, 0.0024, 0.0021, 0.0018, 0.0016, 0.0014,
        0.0012, 0.0011, 0.0009, 0.0008, 0.0007, 0.0006, 0.0005, 0.0005, 0.0004,
        0.0004, 0.0003, 0.0003, 0.0002, 0.0002, 0.0002, 0.0002, 0.0001, 0.0001,
        0.0001])
"""

可以看到，除了 i = 0 外，其余分量上 base = 100000 的值都要比 base = 10000 小。高维度区域的差值很小，也就是说调大 base 后，高维特征几乎没有变化，这对于注意力权重的影响几乎可以忽略不计。

对于 base 性质的研究，与大模型的长度外推息息相关，后续的很多方法都是对 base 做操作，从而影响每个位置对应的旋转角度，进而影响模型的位置编码信息，最终达到长度外推的目的。目前大多长度外推的工作都是通过放大 base 以提升模型的输入长度。

脚本：RoPE 远程衰减特性研究

import os
import math
from typing import List

import torch
import matplotlib.pyplot as plt

os.environ['KMP_DUPLICATE_LIB_OK'] = "True"


def rotate_half(x):
    """Rotates half the hidden dims of the input."""
    x1 = x[..., : x.shape[-1] // 2]
    x2 = x[..., x.shape[-1] // 2 :]
    return torch.cat((-x2, x1), dim=-1)


def generate_qk(base: int, head_dim: int, max_position_embeddings: int = 2048):
    """生成 q、k 向量

    Args:
        base (int): base 值
        head_dim (int): 注意力头的维度
        max_position_embeddings (int, optional): 最大序列长度

    Returns:
        _type_: _description_
    """
    inv_freq = 1.0 / (base ** (torch.arange(0, head_dim, 2, dtype=torch.int64).float() / head_dim))
    t = torch.arange(max_position_embeddings, dtype=torch.int64).type_as(inv_freq)
    
    query_states = torch.ones((1, max_position_embeddings, 8, head_dim)).transpose(1, 2)
    key_states = torch.ones((1, max_position_embeddings, 8, head_dim)).transpose(1, 2)
    position_ids = torch.arange(0, max_position_embeddings, dtype=torch.int64).unsqueeze(0)
    
    inv_freq_expanded = inv_freq[None, :, None].float().expand(position_ids.shape[0], -1, 1)
    position_ids_expanded = position_ids[:, None, :].float()
    freqs = (inv_freq_expanded.float() @ position_ids_expanded.float()).transpose(1, 2)
    emb = torch.cat((freqs, freqs), dim=-1)
    cos = emb.cos()
    sin = emb.sin()
    cos = cos.unsqueeze(1)
    sin = sin.unsqueeze(1)
    q_embed = (query_states * cos) + (rotate_half(query_states) * sin)
    k_embed = (key_states * cos) + (rotate_half(key_states) * sin)
    
    return q_embed, k_embed


def get_matmul(base: int, max_position_embeddings: int) -> List:
    """获取注意力权重矩阵

    Args:
        base (int): base 值
        max_position_embeddings (int): 最大序列长度

    Returns:
        List: 注意力权重矩阵
    """
    q_embed, k_embed = generate_qk(
        base=base,
        head_dim=64,
        max_position_embeddings=max_position_embeddings
    )
    attn_weights = torch.matmul(q_embed, k_embed.transpose(2, 3)) / math.sqrt(64)
    return attn_weights[0][0][0].numpy().tolist()


if __name__ == "__main__":
    max_position_embeddings = 2048

    y = get_matmul(1, max_position_embeddings)
    y1 = get_matmul(10, max_position_embeddings)
    y2 = get_matmul(100, max_position_embeddings)
    y3 = get_matmul(500, max_position_embeddings)
    y4 = get_matmul(5000, max_position_embeddings)
    y5 = get_matmul(10000, max_position_embeddings)
    y6 = get_matmul(50000, max_position_embeddings)
    x = list(range(0, max_position_embeddings))

    plt.rc("figure", figsize=(10, 10))
    plt.plot(x, y, label="base=1")
    plt.plot(x, y1, label="base=10")
    plt.plot(x, y2, label="base=100")
    plt.plot(x, y3, label="base=500")
    plt.plot(x, y4, label="base=5000")
    plt.plot(x, y5, label="base=10000")
    plt.plot(x, y6, label="base=50000")

    # 添加图例
    plt.legend()

    # # 显示图形
    plt.show()

可用于线性 Attention

线性 Attention是一种简化的 Attention 机制，通过使用核函数来近似标准 Attention 中的 softmax 操作，从而将时间复杂度降低为 $O(n)$。比较常见的线性 Attention 是基于特征映射（feature map）的方法，其中一个特征映射 $\phi$ 被应用到 Q 和 K 矩阵上。

$$
LinearAttention(Q, K, V) = \phi(Q)(\phi(K)^TV) \tag{2}
$$

RoPE 的旋转操作是线性可分的，可以在 $\phi(Q)$ 和 $\phi(K)^T$ 上实现旋转操作，从而加上相对位置信息。

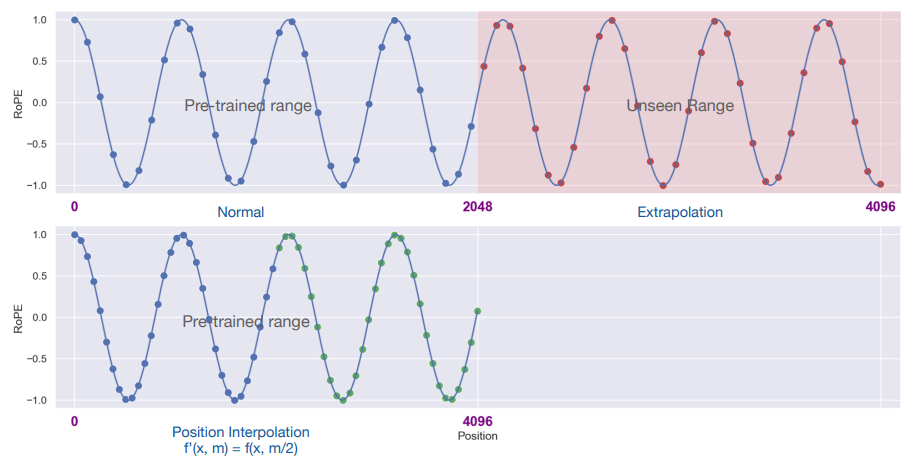
外推效果

虽然 RoPE 理论上可以编码任意长度的绝对位置信息，并且 sin 和 cos 函数计算就能将任意长度的相对位置信息表达出来。但实验发现 RoPE 仍然存在外推问题，即测试长度超过训练长度之后，模型的效果会有显著的崩坏，具体表现为困惑度（PPL）指标显著上升（爆炸）。

参考资料

• 图解 RoPE 旋转位置编码及其特性：https://zhuanlan.zhihu.com/p/667864459
• 再论大模型位置编码及其外推性：https://zhuanlan.zhihu.com/p/675243992