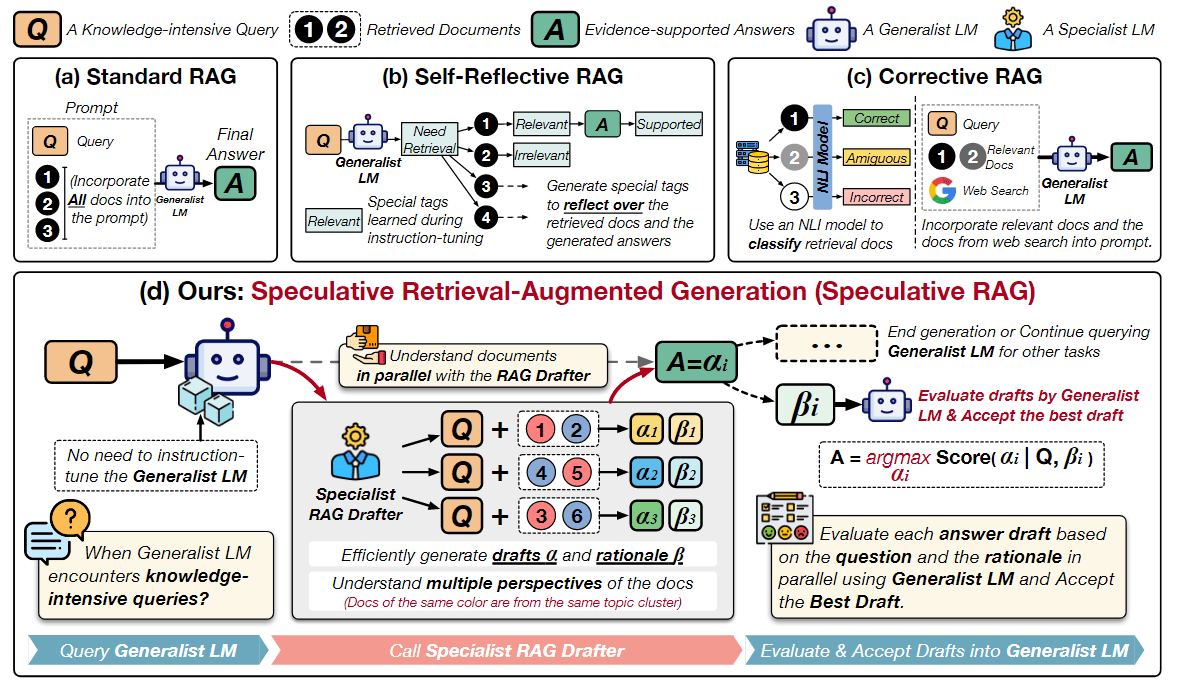
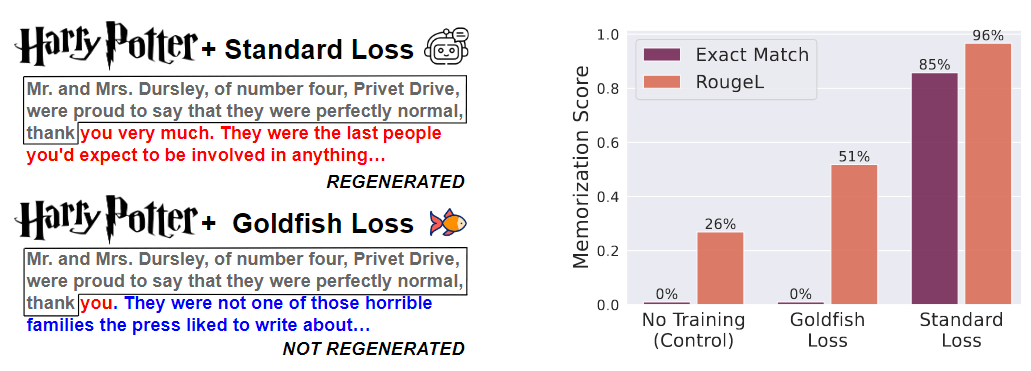
Transformer 架构中的位置编码
Transformer 模型需要位置编码来处理序列数据,因为其核心机制——自注意力(Self-Attention)本身并不具备捕捉序列中元素位置信息的能力。自注意力机制允许模型在计算一个元素的表征时考虑到序列中的所有元素,但是它对这些元素是如何排序的一无所知。这与传统的序列处理模型(如循环神经网络 RNN 和长短期记忆网络 LSTM)不同,后者通过逐个元素的递归处理天然地编码了位置信息。
Transformer 模型的设计理念是完全摒弃递归处理,从而允许并行计算,这极大地提高了训练的效率。然而,这也意味着模型丧失了捕捉序列中位置关系的能力。为了解决这个问题,Transformer 引入了位置编码(Positional Encoding)作为补充信息,确保模型能够利用序列中元素的位置信息。
绝对位置编码
绝对位置编码比较简单,研究者一般会将绝对位置信息加到输入中:在输入的第 k 个向量 $x_k$ 中加入位置向量 $p_k$ 得到 $x_k + p_k$,其中 $p_k$ 仅与 k 相关。计算 $p_k$ 的方法一般有两种:
- 训练式:将位置向量 P 设置为可训练的参数,如 BERT 就将位置向量初始化为 512 x 768 的矩阵,并在训练中更新。但该方法不具备外推性,预训练时设定了句子最大长度后,就无法处理超过该长度的句子。
- 编码式:《Attention is all you need》中提出的 Sinusoidal 位置编码,$p_{i, 2t}$ 表示位置 k 的向量的第 2i 个分量,d 表示向量维度,它显式地编码了位置信息,且具有一定的外推性。
训练式位置编码
训练式位置编码,顾名思义就是每个位置的位置向量会随着模型一起训练。假设模型最大输入长度为 512,向量维度为 768,我们可以初始化一个 [512, 768] 的位置编码矩阵,该矩阵将参与模型的训练,从而学习得到每个位置所对应的向量表征。
问题:如何为每个位置的词向量注入位置信息呢?
答案:将词向量和位置向量相加即可,q 是词向量,$p_m$ 是位置向量。
$$
q_m = f(q, m) = q + p_m
$$
训练式位置编码广泛应用于早期的 Transformer 类型的模型,如 BERT、GPT、ALBERT 等。但其缺点是模型不具有长度外推性,因为位置编码矩阵的大小是预设的,若对其进行扩展,将会破坏模型在预训练阶段学习到的位置信息。例如,将 [512, 768] 扩展为 [1024, 768],新扩展的 512 个位置向量缺少训练,无法正确表示 512 ~ 1023 的位置信息。
Sinusoidal 位置编码
Sinusoidal 位置编码是 Google 在论文《Attention is all you need》中提出的一种绝对位置编码。它的形式如下,其中 d 表示词向量的维度,k 表示位置索引,2i 和 2i + 1 表示位置向量的分量索引,例如 $P_{k, 2i}$ 和 $p_{k,2i+1}$ 分别表示位置 k 的位置向量的第 2i 和第 2i + 1 个分量。
$$
\left{\begin{array}{l}\boldsymbol{p}{k, 2 i}=\sin \left(k / 10000^{2 i / d}\right) \ \boldsymbol{p}{k, 2 i+1}=\cos \left(k / 10000^{2 i / d}\right)\end{array}\right.
$$
从数学形式来看,这是一个具有周期性的三角函数式位置编码,每个分量都是正弦或余弦函数,所以每个分量的数值都具有周期性,并且越靠后的分量,波长越长,频率越低。
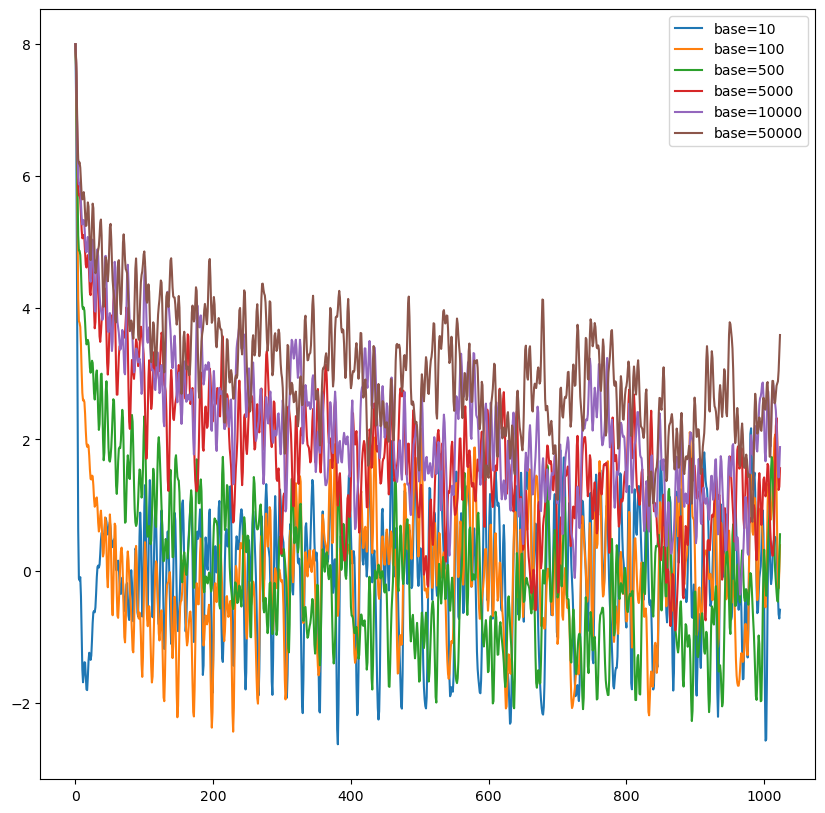
Sinusoidal 位置编码具有远程衰减的性质,具体表现为:对于两个相同的词向量,如果它们之间的距离越近,则它们的内积分数越高,反之则越低。如下图所示,随机初始化两个向量 q 和 k,将 q 固定在位置 0 上,k 的位置从 0 开始逐步变大,依次计算 q 和 k 之间的内积。可以发现,随着 q 和 k 之间的相对距离增加,它们之间的内积分数震荡衰减。
相对位置编码
绝对位置编码计算 Attention 矩阵,m 和 n 分别表示两个位置。
$$
q_m = W_q(x_m + p_m) \quad k_n = W_k(x_n + p_n) \tag{1}
$$
$$
q_mk_n^T = W_q x_m x_n^T W_k^T + W_q x_m p_n^T W_k^T + W_q p_m x_n^T W_k^T + W_q p_m p_n^T W_k^T \tag{2}
$$
可以看到公式(2)中,第一项与位置信息无关,第二项至第四项和位置信息相关。因此,研究者通常是直接修改第二项至第四项的内容,直接在 attention 矩阵中添加相对位置信息。常见的有以下几种方式:
- XLNET 式:将第二项至第四项都做了改变,将 $p_n$ 替换成 sinusoidal 生成式编码 $\hat{R}_{n-m}$,将 $p_m$ 换成两个可以训练的向量 u 和 v。
$$
q_mk_n^T = W_q x_m x_n^T W_k^T + W_q x_m \hat{R}{n-m}^T W_k^T + W_q u x_n^T W_k^T + W_q v \hat{R}{n-m}^T W_k^T \tag{3}
$$
- T5 式:这篇论文的作者认为输入和位置间不应过多的交互,因此将第二项和第三项删除,将第四项替换为一个可学习的偏置 $b_{m, n}$,在 attention 矩阵的基础上加一个可训练的偏置项。
$$
q_m k_n^T = W_q x_m x_n^T W_k^T + b_{m, n} \tag{4}
$$
- DeBerta 式:和 T5 的构造相反,它舍弃了第四项,保留了第二项和第三项,并将位置信息替换成了相对位置编码$\hat{R}_{n-m}$。
$$
q_mk_n^T = W_q x_m x_n^T W_k^T + W_q x_m \hat{R}{n-m}^T W_k^T + W_q \hat{R}{n-m} x_n^T W_k^T \tag{5}
$$
Attention 的核心运算是内积,所以我们希望经过内积的结果能够带有相对信息。也就是说 $q_m$ 和 $k_n$ 的内积仅与输入 $x_m$、$x_n$ 和它们的相对位置 m - n 有关,那么我们可以假设存在函数 g,使得:
$$
q_m k_n^T = g(x_m, x_n, m - n)
$$
此时,我们的目标就是找到这个函数 g,具体方法可参考下文的“相对位置编码方法”。
相对位置编码方法
关于相对位置编码方法,后续会将相应的博客粘贴在此处。
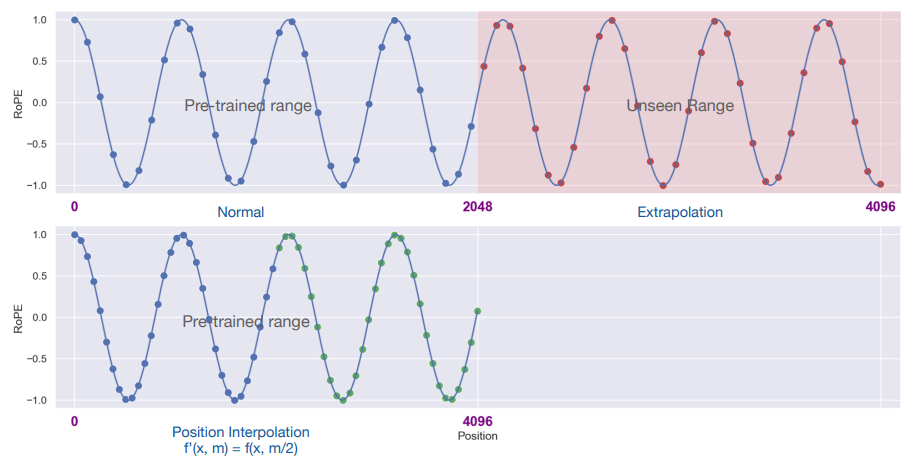
- RoPE:RoPE 相对位置编码解读与外推性研究
- RoPE + 位置线性内插(PI):
- NTK-Aware Scaled RoPE:
- Dynamic NTK RopE:
Q&A
问题:为什么相对位置编码具有外推性?
相对位置编码具有外推性(extrapolation ability)的原因在于它不是将位置信息编码为与序列中的绝对位置直接相关的固定模式,而是将注意力权重或其他模型组件与元素之间的相对距离联系起来。这样,即使在训练时未见过的更长的序列中,模型仍然能够根据学到的相对位置模式进行推断。以下是相对位置编码具有外推性的一些原因:
- 相对距离的一致性:在相对位置编码中,相对距离是一致的,无论元素在序列中的绝对位置如何。因此,模型可以学习到“两个单词相隔一个位置”这样的模式,并将其应用于序列的任何部分。
- 长度不变性:由于相对位置编码关注的是相对距离而非绝对位置,因此它天然不受输入序列长度的影响。这使得模型能够处理比训练时见过的序列更长的序列,而不会丧失对位置关系的理解。
- 泛化能力:相对位置编码使得模型更容易泛化到不同的上下文中,因为它依赖于元素之间的相对关系,而这些关系在不同的文本中是普遍存在的。
- 动态编码:在某些实现中,相对位置信息是动态计算的,而不是像传统的绝对位置编码那样是固定的。这意味着模型可以根据需要为任何给定的序列位置对生成编码,从而提供更大的灵活性和外推能力。
- 适应性强:相对位置编码通常使模型能够更好地适应序列操作,如切割、拼接或排序,因为这些操作不会影响元素之间的相对位置关系。